Máy vectơ hỗ trợ (SVM – viết tắt tên tiếng Anh support vector machine) là một khái niệm trong thống kê và khoa học máy tính cho một tập hợp các phương pháp học có giám sát liên quan đến nhau để phân loại và phân tích hồi quy. SVM dạng chuẩn nhận dữ liệu vào và phân loại chúng vào hai lớp khác nhau. Do đó SVM là một thuật toán phân loại nhị phân. Với một bộ các ví dụ luyện tập thuộc hai thể loại cho trước, thuật toán luyện tập SVM xây dựng một mô hình SVM để phân loại các ví dụ khác vào hai thể loại đó. Một mô hình SVM là một cách biểu diễn các điểm trong không gian và lựa chọn ranh giới giữa hai thể loại sao cho khoảng cách từ các ví dụ luyện tập tới ranh giới là xa nhất có thể. Các ví dụ mới cũng được biểu diễn trong cùng một không gian và được thuật toán dự đoán thuộc một trong hai thể loại tùy vào ví dụ đó nằm ở phía nào của ranh giới.

Mục lục nội dung

Tổng quan về máy vectơ tương hỗ[sửa|sửa mã nguồn]

Một máy vectơ tương hỗ thiết kế xây dựng một siêu phẳng hoặc một tập hợp những siêu phẳng trong một khoảng trống nhiều chiều hoặc vô hạn chiều, hoàn toàn có thể được sử dụng cho phân loại, hồi quy, hoặc những trách nhiệm khác. Một cách trực giác, để phân loại tốt nhất thì những siêu phẳng nằm ở càng xa những điểm tài liệu của tổng thể những lớp ( gọi là hàm lề ) càng tốt, vì nói chung lề càng lớn thì sai số tổng quát hóa của thuật toán phân loại càng bé .

Trong nhiều trường hợp, không thể phân chia các lớp dữ liệu một cách tuyến tính trong một không gian ban đầu được dùng để mô tả một vấn đề. Vì vậy, nhiều khi cần phải ánh xạ các điểm dữ liệu trong không gian ban đầu vào một không gian mới nhiều chiều hơn, để việc phân tách chúng trở nên dễ dàng hơn trong không gian mới. Để việc tính toán được hiệu quả, ánh xạ sử dụng trong thuật toán SVM chỉ đòi hỏi tích vô hướng của các vectơ dữ liệu trong không gian mới có thể được tính dễ dàng từ các tọa độ trong không gian cũ. Tích vô hướng này được xác định bằng một hàm hạt nhân K(x,y) phù hợp.[1] Một siêu phẳng trong không gian mới được định nghĩa là tập hợp các điểm có tích vô hướng với một vectơ cố định trong không gian đó là một hằng số. Vectơ xác định một siêu phẳng sử dụng trong SVM là một tổ hợp tuyến tính của các vectơ dữ liệu luyện tập trong không gian mới với các hệ số αi. Với siêu phẳng lựa chọn như trên, các điểm x trong không gian đặc trưng được ánh xạ vào một siêu mặt phẳng là các điểm thỏa mãn:

Σi αi K(xi,x) = hằng số.

Ghi chú rằng nếu K(x,y) nhận giá trị ngày càng nhỏ khi y xa dần khỏi x thì mỗi số hạng của tổng trên được dùng để đo độ tương tự giữa x với điểm xi tương ứng trong dữ liệu luyện tập. Như vậy, tác dụng của tổng trên chính là so sánh khoảng cách giữa điểm cần dự đoán với các điểm dữ liệu đã biết. Lưu ý là tập hợp các điểm x được ánh xạ vào một siêu phẳng có thể có độ phức tạp tùy ý trong không gian ban đầu, nên có thể phân tách các tập hợp thậm chí không lồi trong không gian ban đầu.

Bạn đang đọc: Máy vectơ hỗ trợ – Wikipedia tiếng Việt

Thuật toán SVM bắt đầu được tìm ra bởi Vladimir N. Vapnik và dạng chuẩn lúc bấy giờ sử dụng lề mềm được tìm ra bởi Vapnik và Corinna Cortes năm 1995. [ 2 ]

Đặt yếu tố[sửa|sửa mã nguồn]

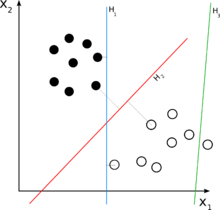H3 ( màu xanh lá cây ) không chia tách hai lớp tài liệu. H1 ( màu xanh lơ ) phân tách hai lớp với lề nhỏ và H2 ( màu đỏ ) phân tách với lề cực lớn .

Phân loại thống kê là một nhiệm vụ phổ biến trong học máy. Trong mô hình học có giám sát, thuật toán được cho trước một số điểm dữ liệu cùng với nhãn của chúng thuộc một trong hai lớp cho trước. Mục tiêu của thuật toán là xác định xem một điểm dữ liệu mới sẽ được thuộc về lớp nào. Mỗi điểm dữ liệu được biểu diễn dưới dạng một vector p-chiều, và ta muốn biết liệu có thể chia tách hai lớp dữ liệu bằng một siêu phẳng p − 1 chiều. Đây gọi là phân loại tuyến tính. Có nhiều siêu phẳng có thể phân loại được dữ liệu. Một lựa chọn hợp lý trong chúng là siêu phẳng có lề lớn nhất giữa hai lớp.

SVM tuyến tính[sửa|sửa mã nguồn]

Ta có một tập huấn luyện

{\displaystyle {\mathcal {D}}}

${\mathcal {D}}$ gồm n điểm có dạng

{\mathcal {D}}=\left\{(\mathbf {x} _{i},y_{i})\mid \mathbf {x} _{i}\in \mathbb {R} ^{p},\,y_{i}\in \{-1,1\}\right\}_{i=1}^{n}

với yi mang giá trị 1 hoặc −1, xác định lớp của điểm

{\displaystyle \mathbf {x} _{i}}

$\mathbf {x} _{i}$ . Mỗi

{\displaystyle \mathbf {x} _{i}}

là một vectơ thực p-chiều. Ta cần tìm siêu phẳng có lề lớn nhất chia tách các điểm có

=
1

{\displaystyle y_{i}=1}

$y_{i}=1$ và các điểm có

=
−
1

{\displaystyle y_{i}=-1}

$y_{i}=-1$ . Mỗi siêu phẳng đều có thể được viết dưới dạng một tập hợp các điểm

{\displaystyle \mathbf {x} }

$\mathbf {x}$ thỏa mãn

Siêu phẳng với lề cực lớn cho một SVM phân tách tài liệu thuộc hai lớp. Các ví dụ nằm trên lề được gọi là những vectơ tương hỗ .

\mathbf {w} \cdot \mathbf {x} -b=0,\,

với

⋅

{\displaystyle \cdot }

$\cdot$ ký hiệu cho tích vô hướng và

{\displaystyle {\mathbf {w} }}

${\mathbf {w} }$ là một vectơ pháp tuyến của siêu phẳng. Tham số

‖

{\displaystyle {\tfrac {b}{\|\mathbf {w} \|}}}

${\tfrac {b}{\|\mathbf {w} \|}}$ xác định khoảng cách giữa gốc tọa độ và siêu phẳng theo hướng vectơ pháp tuyến

{\displaystyle {\mathbf {w} }}

Chúng ta cần chọn

{\displaystyle {\mathbf {w} }}

và

{\displaystyle b}

$b$ để cực đại hóa lề, hay khoảng cách giữa hai siêu mặt song song ở xa nhau nhất có thể trong khi vẫn phân chia được dữ liệu. Các siêu mặt ấy được xác định bằng

\mathbf {w} \cdot \mathbf {x} -b=1\,

và

\mathbf {w} \cdot \mathbf {x} -b=-1.\,

Để ý rằng nếu dữ liệu huấn luyện có thể được chia tách một cách tuyến tính, thì ta có thể chọn hai siêu phẳng của lề sao cho không có điểm nào ở giữa chúng và sau đó tăng khoảng cách giữa chúng đến tối đa có thể. Bằng hình học, ta tìm được khoảng cách giữa hai siêu phẳng là

‖

{\displaystyle {\tfrac {2}{\|\mathbf {w} \|}}}

${\tfrac {2}{\|\mathbf {w} \|}}$ . Vì vậy ta muốn cực tiểu hóa giá trị

‖

{\displaystyle \|\mathbf {w} \|}

$\|\mathbf {w} \|$ . Để đảm bảo không có điểm dữ liệu nào trong lề, ta thêm vào các điều kiện sau:

Với mỗi

{\displaystyle i}

$i$ ta có

\mathbf {w} \cdot \mathbf {x} _{i}-b\geq 1\qquad {\text{ cho }}\mathbf {x} _{i}

hoặc

\mathbf {w} \cdot \mathbf {x} _{i}-b\leq -1\qquad {\text{ cho }}\mathbf {x} _{i}

Có thể viết gọn lại như sau với mọi

1
≤
i
≤
n

{\displaystyle 1\leq i\leq n}

$1\leq i\leq n$ :

y_{i}(\mathbf {w} \cdot \mathbf {x} _{i}-b)\geq 1,\qquad \qquad (1)

Tóm lại, ta có bài toán tối ưu hóa sau :

Cực tiểu hóa (theo

,
b

{\displaystyle {\mathbf {w} ,b}}

${\mathbf {w} ,b}$ )

‖ w ‖ { \ displaystyle \ | \ mathbf { w } \ | }

với điều kiện (với mọi

i
=
1
,
…
,
n

{\displaystyle i=1,\dots ,n}

$i=1,\dots ,n$ )

y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)\geq 1.\,

Dạng bắt đầu[sửa|sửa mã nguồn]

Bài toán tối ưu ở mục trên tương đối khó giải vì hàm mục tiêu phụ thuộc vào ||w||, là một hàm có khai căn. Tuy nhiên có thể thay ||w|| bằng hàm mục tiêu

1
2

‖

{\displaystyle {\tfrac {1}{2}}\|\mathbf {w} \|^{2}}

${\tfrac {1}{2}}\|\mathbf {w} \|^{2}$ (hệ số 1/2 để tiện cho các biến đổi toán học sau này) mà không làm thay đổi lời giải (lời giải của bài toán mới và bài toán ban đầu có cùng w và b). Đây là một bài toán quy hoạch toàn phương. Cụ thể hơn:

Cực tiểu hóa ( theo w, b { \ displaystyle { \ mathbf { w }, b } } )

{\frac {1}{2}}\|\mathbf {w} \|^{2}

với điều kiện kèm theo ( với mọi i = 1, …, n { \ displaystyle i = 1, \ dots, n } )

y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)\geq 1.

Bằng cách thêm các nhân tử Lagrange

{\displaystyle {\boldsymbol {\alpha }}}

${\boldsymbol {\alpha }}$ , bài toán trên trở thành

\min _{\mathbf {w} ,b}\max _{{\boldsymbol {\alpha }}\geq 0}\left\{{\frac {1}{2}}\|\mathbf {w} \|^{2}-\sum _{i=1}^{n}{\alpha _{i}[y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1]}\right\}

nghĩa là ta cần tìm một điểm yên ngựa. Khi đó, tất cả các điểm không nằm trên lề, nghĩa là

(

⋅

−
b
)
−
1
>
0

{\displaystyle y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1>0}

${\displaystyle y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1>0}” class=”mwe-math-fallback-image-inline” src=”https://wikimedia.org/api/rest_v1/media/math/render/svg/5467f90783498a0862c58150ba32c4c14f6f3f96″/> đều không ảnh hưởng đến giá trị hàm mục tiêu vì ta có thể chọnαi{\displaystyle \alpha _{i}}<img data-lazyloaded=$ bằng không.

Có thể giải bài toán này bằng những kĩ thuật thường thì cho quy hoạch toàn phương. Theo điều kiện kèm theo Karush – Kuhn – Tucker, giải thuật hoàn toàn có thể được viết dưới dạng tổng hợp tuyến tính của những vectơ rèn luyện

\mathbf {w} =\sum _{i=1}^{n}{\alpha _{i}y_{i}\mathbf {x_{i}} }.

Chỉ có một vài

{\displaystyle \alpha _{i}}

nhận giá trị lớn hơn 0. Các điểm

{\displaystyle \mathbf {x_{i}} }

$\mathbf {x_{i}}$ tương ứng là các vectơ hỗ trợ nằm trên lề và thỏa mãn

(

⋅

−
b
)
=
1

{\displaystyle y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)=1}

$y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)=1$ . Từ điều kiện này, ta nhận thấy

\mathbf {w} \cdot \mathbf {x_{i}} -b=1/y_{i}=y_{i}\iff b=\mathbf {w} \cdot \mathbf {x_{i}} -y_{i}

từ đó ta suy ra được giá trị

{\displaystyle b}

. Trên thực tế, một cách thức tốt hơn để tính

{\displaystyle b}

là tính giá trị trung bình từ tất cả

S
V

{\displaystyle N_{SV}}

$N_{SV}$ vectơ hỗ trợ:

b={\frac {1}{N_{SV}}}\sum _{i=1}^{N_{SV}}{(\mathbf {w} \cdot \mathbf {x_{i}} -y_{i})}

Dạng đối ngẫu[sửa|sửa mã nguồn]

Nếu viết điều kiện phân loại dưới dạng đối ngẫu không điều kiện thì sẽ dễ dàng nhận thấy siêu phẳng với lề lớn nhất, và do đó nhiệm vụ phân loại, chỉ phụ thuộc vào các điểm luyện tập nằm trên lề, còn gọi là các vectơ hỗ trợ.

Vì

‖

=
w
⋅
w

{\displaystyle \|\mathbf {w} \|^{2}=w\cdot w}

$\|\mathbf {w} \|^{2}=w\cdot w$ và

∑

i
=
1

{\displaystyle \mathbf {w} =\sum _{i=1}^{n}{\alpha _{i}y_{i}\mathbf {x_{i}} }}

$\mathbf {w} =\sum _{i=1}^{n}{\alpha _{i}y_{i}\mathbf {x_{i}} }$ , ta nhận thấy bài toán đối ngẫu của SVM là chính là bài toán tối ưu hóa sau:

Cực đại hóa ( theo α i { \ displaystyle \ alpha _ { i } } )

{\tilde {L}}(\mathbf {\alpha } )=\sum _{i=1}^{n}\alpha _{i}-{\frac {1}{2}}\sum _{i,j}\alpha _{i}\alpha _{j}y_{i}y_{j}\mathbf {x} _{i}^{T}\mathbf {x} _{j}=\sum _{i=1}^{n}\alpha _{i}-{\frac {1}{2}}\sum _{i,j}\alpha _{i}\alpha _{j}y_{i}y_{j}k(\mathbf {x} _{i},\mathbf {x} _{j})

với điều kiện kèm theo ( với mọi i = 1, …, n { \ displaystyle i = 1, \ dots, n } )

\alpha _{i}\geq 0,\,

và điều kiện kèm theo sau ứng với việc cực tiểu hóa theo b { \ displaystyle b }

\sum _{i=1}^{n}\alpha _{i}y_{i}=0.

Ở đây hàm hạt nhân được định nghĩa là

k
(

)
=

⋅

{\displaystyle k(\mathbf {x} _{i},\mathbf {x} _{j})=\mathbf {x} _{i}\cdot \mathbf {x} _{j}}

$k(\mathbf {x} _{i},\mathbf {x} _{j})=\mathbf {x} _{i}\cdot \mathbf {x} _{j}$ .

Sau khi giải xong, có thể tính

{\displaystyle \mathbf {w} }

$\mathbf {w}$ từ các giá trị

{\displaystyle \alpha }

$\alpha$ tìm được như sau:

\mathbf {w} =\sum _{i}\alpha _{i}y_{i}\mathbf {x} _{i}.

Năm 1995, Corinna Cortes và Vladimir N. Vapnik đề xuất một ý tưởng mới cho phép thuật toán gán nhãn sai cho một số ví dụ luyện tập.[2] Nếu không tồn tại siêu phẳng nào phân tách được hai lớp dữ liệu, thì thuật toán lề mềm sẽ chọn một siêu phẳng phân tách các ví dụ luyện tập tốt nhất có thể, và đồng thời cực đại hóa khoảng cách giữa siêu phẳng với các ví dụ được gán đúng nhãn. Phương pháp này sử dụng các biến bù

{\displaystyle \xi _{i}}

$\xi _{i}$ , dùng để đo độ sai lệch của ví dụ

{\displaystyle x_{i}}

$x_{i}$

y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)\geq 1-\xi _{i}\quad 1\leq i\leq n.\quad \quad (2)

Hàm mục tiêu có thêm 1 số ít hạng mới để phạt thuật toán khi ξ i { \ displaystyle \ xi _ { i } } khác không, và bài toán tối ưu hóa trở thành việc trao đổi giữa lề lớn và mức phạt nhỏ. Nếu hàm phạt là tuyến tính thì bài toán trở thành :

\min _{\mathbf {w} ,\mathbf {\xi } ,b}\left\{{\frac {1}{2}}\|\mathbf {w} \|^{2}+C\sum _{i=1}^{n}\xi _{i}\right\}

với điều kiện (với mọi

i
=
1
,
…
n

{\displaystyle i=1,\dots n}

$i=1,\dots n$ )

y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)\geq 1-\xi _{i},~~~~\xi _{i}\geq 0

Có thể giải bài toán trên bằng nhân tử Lagrange tương tự như như trường hợp cơ bản ở trên. Bài toán cần giải trở thành :

\min _{\mathbf {w} ,\mathbf {\xi } ,b}\max _{{\boldsymbol {\alpha }},{\boldsymbol {\beta }}}\left\{{\frac {1}{2}}\|\mathbf {w} \|^{2}+C\sum _{i=1}^{n}\xi _{i}-\sum _{i=1}^{n}{\alpha _{i}[y_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1+\xi _{i}]}-\sum _{i=1}^{n}\beta _{i}\xi _{i}\right\}

với

≥
0

{\displaystyle \alpha _{i},\beta _{i}\geq 0}

$\alpha _{i},\beta _{i}\geq 0$ .

Dạng đối ngẫu[sửa|sửa mã nguồn]

Cực đại hóa ( theo α i { \ displaystyle \ alpha _ { i } } )

{\tilde {L}}(\mathbf {\alpha } )=\sum _{i=1}^{n}\alpha _{i}-{\frac {1}{2}}\sum _{i,j}\alpha _{i}\alpha _{j}y_{i}y_{j}k(\mathbf {x} _{i},\mathbf {x} _{j})

với điều kiện kèm theo ( với mọi i = 1, …, n { \ displaystyle i = 1, \ dots, n } )

0\leq \alpha _{i}\leq C,\,

và

∑ i = 1 n α i y i = 0. { \ displaystyle \ sum _ { i = 1 } ^ { n } \ alpha _ { i } y_ { i } = 0. }

Ưu điểm của việc dùng hàm phạt tuyến tính là các biến bù biến mất khỏi bài toán đối ngẫu, và hằng số C chỉ xuất hiện dưới dạng một chặn trên cho các nhân tử Lagrange. Cách đặt vấn đề trên đã mang lại nhiều thành quả trong thực tiễn, và Cortes và Vapnik đã nhận được giải Paris Kanellakis của ACM năm 2008 cho đóng góp này.[3] Các hàm phạt phi tuyến cũng được sử dụng, đặc biệt là để giảm ảnh hưởng của các trường hợp ngoại lệ, tuy nhiên nếu không lựa chọn hàm phạt cẩn thận thì bài toán trở thành không lồi, và việc tìm lời giải tối ưu toàn cục thường là rất khó.