y = |x|Đồ thị hàm số

Giá trị tuyệt đối (tiếng Anh: Absolute value) – còn thường được gọi là mô-đun (modulus) của một số thực x được viết là |x|, là giá trị của nó nhưng bỏ dấu. Như vậy |x| = –x nếu x là số âm (-x là số dương), và |x| = x nếu x là số dương, và |0| =0. Giá trị tuyệt đối của một số có thể hiểu là khoảng cách của số đó đến số 0.

Trong toán học, việc sử dụng giá trị tuyệt đối có trong hàng loạt hàm toán học, và còn được lan rộng ra cho những số phức, véctơ, trường, … liên hệ mật thiết với khái niệm giá trị .

Đồ thị của một hàm số có các biến số nằm trong dấu “giá trị tuyệt đối” thì luôn luôn nằm phía trên của trục hoành.

Bạn đang đọc: Giá trị tuyệt đối – Wikipedia tiếng Việt

Với mọi số thực

{\displaystyle a}

$a$ , giá trị tuyệt đối của

{\displaystyle a}

– ký hiệu là

{\displaystyle |a|}

$|a|$ – được định nghĩa:

|a| = \begin{cases} a, & \mbox{n}\acute{\hat{\mbox{e}}}\mbox{u}\ a \ge 0 \\ -a, & \mbox{n}\acute{\hat{\mbox{e}}}\mbox{u}\ a < 0. \end{cases}

Định nghĩa trên cho thấy, giá trị tuyệt đối của a { \ displaystyle a } luôn là 1 số ít không âm .
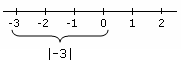Giá trị tuyết đối của – 3 là khoảng cách từ điểm – 3 đến điểm 0 trên đường thẳng thực .

Xem thêm: phân vân trong tiếng Tiếng Anh - Tiếng Việt-Tiếng Anh

Hiểu theo góc độ hình học, giá trị tuyệt đối của một số thực là khoảng cách từ số đó đến điểm 0 trên đường thẳng thực (real number line, còn gọi là trục số thực). Tổng quát hơn, giá trị tuyệt đối giữa hai số thực khác nhau là khoảng cách giữa chúng trên đường thẳng thực, ví dụ: |5 – 3| = 2 (khoảng cách giữa 5 và 3).

Mệnh đề 1 dưới đây là một đồng nhất thức (identity). Nó tương đương với định nghĩa trên và đôi khi có thể được sử dụng để định nghĩa về giá trị tuyệt đối.

MỆNH ĐỀ 1:

|a| = \sqrt{a^2}

MỆNH ĐỀ 2:

|a| \ge 0

Tính không âm

$|a| = 0 \iff a = 0$
Xác định tính dương

$|ab| = |a||b|\,$
Tính kết hợp
$|a+b| \le |a| + |b|$
Subadditivity

Chứng minh :

Nếu $a { \ displaystyle a }$ $b$ 0, chẳng hạn:

a=0 \iff |a+b|=|0+b|=|0|+|b|=|a|+|b|

Nếu $a { \ displaystyle a }$ $b { \ displaystyle b }$

|a+b|=|a|+|b|

Nếu
a
{\displaystyle a}
Xem thêm: Clingme là gì? Hướng dẫn sử dụng App Clingme hoàn tiền [2021]
$b { \ displaystyle b }$
- Với $|a| \ge |b| \iff |a+b|=|a|-|b|$
- Với $|a| \le |b| \iff |a+b|=|b|-|a|$

Vì

{\displaystyle |a|}

và

{\displaystyle |b|}

$|b|$ đều lớn hơn 0 nên

−

{\displaystyle |a|-|b|}

$|a|-|b|$ hoặc

−

{\displaystyle |b|-|a|}

$|b|-|a|$ đều nhỏ hơn tổng

{\displaystyle |a|+|b|}

$|a|+|b|$ .
Vậy ta luôn có:

a
+
b

≤

{\displaystyle |a+b|\leq |a|+|b|}

MỆNH ĐỀ 3:

|-a| = |a|\,

Tính đối xứng

|a - b| = 0 \iff a = b

Đẳng thức indiscernibles (tương đương với xác định dương)

$|a - b| \le |a - c| +|c - b|$
Bất đẳng thức tam giác (tương đương với subadditivity)

$|a/b| = |a| / |b|\ \mbox{n}\acute{\hat{\mbox{e}}}\mbox{u}\ b \ne 0) \,$
Bảo toàn trong phép chia (tương đương với multiplicativeness)

$|a-b| \ge |a| - |b|$
Điều phải chứng minh (Articles need to prove)

Ta cũng có hai bất đẳng thức (inequalities) quan trọng:

|a| \le b \iff -b \le a \le b

|a|\geq b\iff a\leq -b\ {\mbox{hoặc}}\ b\leq a

Hai bất đẳng thức trên thường được sử dụng để giải những bài toán bất đẳng thức khác. Ví dụ :

|x-3| \le 9

\iff -9 \le x-3 \le 9

\iff -6 \le x \le 12

Vì số phức (complex number) không có thứ tự, nên định nghĩa về giá trị tuyệt đối của các số phức không thể được suy ra từ định nghĩa tương ứng của các số thực. Tuy nhiên, từ đồng nhất thức ở mệnh đề 1 (xem phần số thực ở trên), ta có định nghĩa sau:

Biểu diễn véc tơ số phức z = x + iyVới mọi số phức :