Nghiệm nguyên là gì? Phân biệt giữa số nguyên và số thực

Trong quá trình giải toán học, nhiều người thắc mắc không biết nghiệm nguyên là gì? Cũng như chưa hiểu rõ về số nguyên và số thực. Hãy cùng Mindovermetal đi tìm câu trả lời cho những câu hỏi ở trên ngay trong bài viết sau đây.

Nghiệm Nguyên là gì?

Có rất nhiều người thắc mắc cũng như đã quên mất nghiệm nguyên là gì. Thực chất, nghiệm nguyên chính là cách gọi chung cho số nguyên và số thực. Vậy số nguyên và số thực là gì?

Số Nguyên là gì?

Định nghĩa

Số nguyên là tập hợp gồm có số không, số tự nhiên dương và các số đối của chúng gọi là số tự nhiên âm. Tập hợp số nguyên là không giới hạn nhưng vẫn có thể đếm được. Số nguyên âm được ký hiệu là Z.

Số nguyên được chia làm 2 loại. Bao gồm:

• Số nguyên dương: là tập hợp các số nguyên lớn hơn 0, được ký hiệu là Z+.
  Ví dụ: 3, 4, 5, 6, 7,…
• Số nguyên âm: là tập hợp các số nguyên nhỏ hơn 0, được ký hiệu là Z-.
  Ví dụ: -3, -4, -5, -6, -7,…

Lưu ý: Tập hợp các số nguyên dương hay số nguyên âm đều không bao gồm số không.

Tính chất

Các tính chất cơ bản của số nguyên gồm có:

• Không có số nguyên nào là lớn nhất hay là nhỏ nhất.
• Số nguyên dương nhỏ nhất là 1, số nguyên âm nhỏ nhất là -1.
• Số nguyên Z có tập hợp con hữu hạn luôn có phần tử lớn nhất và phần tử nhỏ nhất.
• Không có số nguyên nào nằm giữa hai số nguyên liên tiếp.

Số thực là gì?

Định nghĩa

Số thực là tập hợp bao gồm các số nguyên, số hữu tỉ và số vô tỉ. Tức là số nguyên là tập hợp con của số thực. Số thực được biểu diễn trên trục số dài vô hạn và được ký hiệu là R.

Tập hợp số thực được diễn tả qua hình sau:

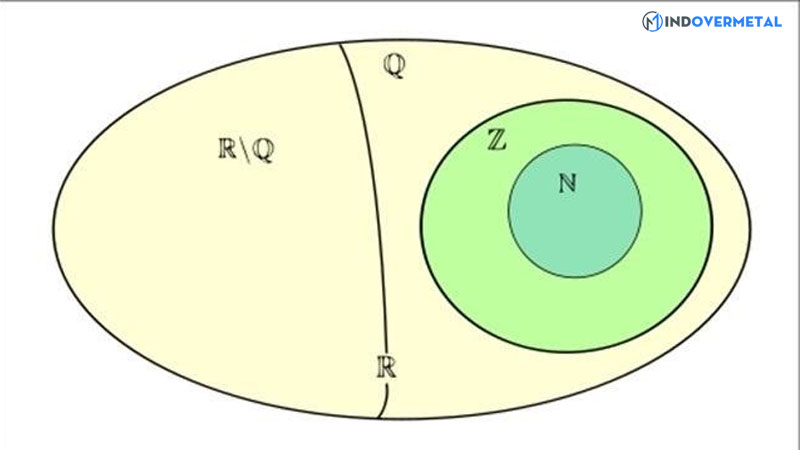
Trong đó:

N : Tập hợp số tự nhiên
Z : Tập hợp số nguyên
Q : Tập hợp số hữu tỉ
I = RQ : Tập hợp số vô tỉ

Tính chất

Các tính chất cơ bản của số thực bao gồm:

• Số nguyên chỉ là tập con của số thực.
• Tổng, tích của hai số thực không âm cũng là một số thực không âm.
• Số thực là tập hợp vô hạn các số vô cùng nhiều không đếm được.
• Số thực có hệ thống các tập con vô hạn có thể đếm được như số nguyên, số hữu tỷ, số tính được,…
• Bất kỳ số thực khác không đều là số âm hoặc số dương.
• Số thực có thể biểu diễn bằng thập phân
• Số thực có thể được dùng để thực hiện các phép đo đại lượng liên tục.
• Sự khác nhau giữa số nguyên và số thực
• Số nguyên là tập hợp số đếm được, còn số thực thì không đếm được.
• Số nguyên chỉ tập hợp số tự nhiên, còn số thực tập hợp rất nhiều số.

Một số phương pháp giải trình nghiệm nguyên

Phương trình nghiệm nguyên là một dạng bài tập toán học có độ khó cao. Còn tùy thuộc vào từng bài tập mà ta sẽ áp dụng một hay là nhiều phương pháp cùng 1 lúc để có thể giải được bài toán đó. Dưới đây là 10 phương pháp giải trình nghiệm nguyên mà bạn cần biết:

• Sử dụng tính chẵn lẻ
• Phương pháp phân tích
• Phương pháp cực hạn
• Dùng chia hết và có số dư
• Phương pháp loại trừ
• Sử dụng tính chất của số nguyên tố
• Phương pháp đưa về dạng tổng
• Sử dụng tính chất nghiệm của phương trình bậc 2
• Phương pháp lùi vô hạn
• Phương pháp dùng bất đẳng thức

Lưu ý khi giải phương trình nghiệm nguyên:

Trong quá trình giải các phương trình nghiệm nguyên, ta cần phải biết cách áp dụng linh hoạt các phương pháp như chia hết, tính chẵn lẻ hay có dư,… mới mục đích là tìm ra được điểm đặc biệt của các ẩn số, cũng như tìm ra được những biểu thức có chứa ẩn trong phương trình.

Chỉ có như vậy thì bạn mới có thể đưa phương trình đó về dưới các dạng phương trình đơn giản hơn, để có thể giải được phương trình 1 cách dễ dàng.

Hy vọng thông qua bài viết này, các bạn sẽ nắm vững kiến thức về Nghiệm Nguyên là gì? Cũng như hiểu rõ sự khác biệt giữa số thực và số nguyên. Nếu còn điều gì các bạn chưa rõ, hãy bình luận xuống phía dưới để Mindovermetal giải đáp nhé! Chúc các bạn học tốt.