Dao động điều hòa đơn giản (hay dao động điều hòa đơn tần, hay đôi khi được gọi ngắn gọn là dao động điều hòa) là một dao động có ly độ biến thiên theo thời gian theo hàm điều hòa và ở tần số và biên độ không đổi theo thời gian. Vị trí của một vật chuyển động theo dao động điều hòa đơn, x(t) có thể biểu diễn phụ thuộc vào thời gian t theo công thức:
- x ( t ) = A cos ( 2 π f t + ϕ ), { \ displaystyle x ( t ) = A \ cos \ left ( 2 \ pi \ ! ft + \ phi \ right ), }
Với A là biên độ, f là tần số, φ là pha.
Mọi chuyển động có biên độ biến đổi theo thời gian một cách tuần hoàn, đều có thể được phân tích thành tổng các biến đổi theo dao động điều hòa đơn, sau khi áp dụng biến đổi Fourier.
Bạn đang đọc: Dao động điều hòa đơn giản – Wikipedia tiếng Việt
Dao động điều hòa đơn thể hiện sóng đơn sắc hay đơn tần. Nguồn gốc của chữ đơn sắc là sóng điện từ trong giải phổ ánh sáng nếu có điện trường và từ trường tại một vị trí dao động điều hòa đơn (ở một tần số duy nhất) thì ứng với một màu sắc và là ánh sáng đơn sắc.
Phương trình động lực học của dao động điều hòa đơn thuần[sửa|sửa mã nguồn]
Ví dụ một lò xo khi bị kéo (hay nén) một khoảng y khỏi vị trí cân bằng sẽ sinh ra lực đàn hồi khiến lò xo quay trở về vị trí cân bằng:
- F = − k y { \ displaystyle F = – ky \, }
với k là hệ số đàn hồi của lò xo.
Lực này gây nên gia tốc chuyển động a cho vật thể khối lượng m treo trên lò xo
- F = m a { \ displaystyle F = ma \, }
Do đó :
- m a = − k y { \ displaystyle ma = – ky \, }
- m d 2 y d t 2 = − k y { \ displaystyle m { \ frac { \ mathrm { d } ^ { 2 } y } { \ mathrm { d } t ^ { 2 } } } = – ky }
( 1 ) { \ displaystyle ( 1 ) \, }
(
1
)
{\displaystyle (1)\,}
có phương trình đặc trưng
u
2
=
−
k
m
=
−
ω
2
{\displaystyle u^{2}=-{\frac {k}{m}}=-\omega ^{2}\,}
Có nghiệm phức
u
=
±
ω
i
{\displaystyle u=\pm \omega i\,}
Từ công thức nghiệm tổng quát:
y
(
t
)
=
e
α
t
(
c
1
cos
(
β
t
)
+
c
2
sin
(
β
t
)
)
{\displaystyle y(t)=e^{\alpha t}\left(c_{1}\cos \left(\beta t\right)+c_{2}\sin \left(\beta t\right)\right)\,}

α
{\displaystyle \alpha \,}

β
{\displaystyle \beta \,}

Tìm được một nghiệm đơn thuần của phương trình trên
- y ( t ) = c 1 cos ( ω t ) + c 2 sin ( ω t ) = c 1 2 + c 2 2 ( c 1 c 1 2 + c 2 2 cos ( ω t ) + c 2 c 1 2 + c 2 2 sin ( ω t ) ) { \ displaystyle y ( t ) = c_ { 1 } \ cos \ left ( \ omega t \ right ) + c_ { 2 } \ sin \ left ( \ omega t \ right ) = { \ sqrt { { c_ { 1 } } ^ { 2 } + { c_ { 2 } } ^ { 2 } } } \ left ( { \ frac { c_ { 1 } } { \ sqrt { { c_ { 1 } } ^ { 2 } + { c_ { 2 } } ^ { 2 } } } } \ cos \ left ( \ omega t \ right ) + { \ frac { c_ { 2 } } { \ sqrt { { c_ { 1 } } ^ { 2 } + { c_ { 2 } } ^ { 2 } } } } \ sin \ left ( \ omega t \ right ) \ right ) }
- = A cos ( ω t + φ ) { \ displaystyle = A \ cos \ left ( \ omega t + \ varphi \ right ) \, }
- = A cos ( ω t + φ ) { \ displaystyle = A \ cos \ left ( \ omega t + \ varphi \ right ) \, }
với
- ω = k m, { \ displaystyle \ omega = { \ sqrt { \ frac { k } { m } } }, }
- A = c 1 2 + c 2 2, { \ displaystyle A = { \ sqrt { { c_ { 1 } } ^ { 2 } + { c_ { 2 } } ^ { 2 } } }, }
- tan φ = ( c 2 c 1 ), { \ displaystyle \ tan \ varphi = \ left ( { \ frac { c_ { 2 } } { c_ { 1 } } } \ right ), }
ở đây :
- c 1 { \ displaystyle c_ { 1 } \, }
c 2 { \ displaystyle c_ { 2 } \, }
A { \ displaystyle A \, }
ω { \ displaystyle \ omega \, }
tần số góc, φ { \ displaystyle \ varphi \, }
pha ban đầu.
Vận tốc và tần suất của vật thể dao động điều hòa được tính bằng đạo hàm bậc nhất và bậc hai của li độ :
- v ( t ) = d y d t = − A ω sin ( ω t + φ ), { \ displaystyle v ( t ) = { \ frac { \ mathrm { d } y } { \ mathrm { d } t } } = – A \ omega \ sin ( \ omega t + \ varphi ), }
- a ( t ) = d 2 y d t 2 = − A ω 2 cos ( ω t + φ ) = − ω 2 y. { \ displaystyle a ( t ) = { \ frac { \ mathrm { d } ^ { 2 } y } { \ mathrm { d } t ^ { 2 } } } = – A \ omega ^ { 2 } \ cos ( \ omega t + \ varphi ) = – \ omega ^ { 2 } y. }
Năng lượng trong dao động điều hòa đơn thuần[sửa|sửa mã nguồn]
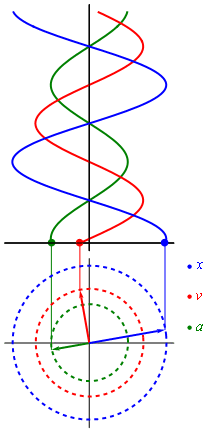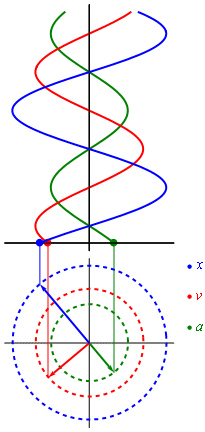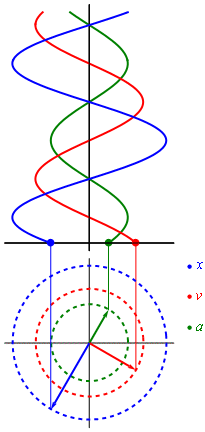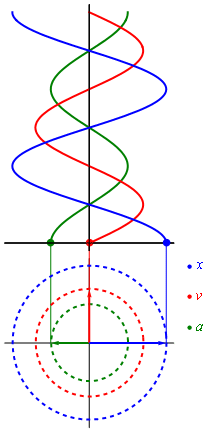 Biểu diễn li độ, tốc độ, tần suất theo pha dao động. Ở đây ta thấy li độ ngược pha với tần suất, li độ và tần suất cùng vuông pha với tốc độ
Biểu diễn li độ, tốc độ, tần suất theo pha dao động. Ở đây ta thấy li độ ngược pha với tần suất, li độ và tần suất cùng vuông pha với tốc độ
Động năng
E
d
{\displaystyle E_{d}\,}

- E d = 1 2 m v ( t ) 2 = 1 2 m ω 2 A 2 sin 2 ( ω t + φ ) = 1 2 k A 2 sin 2 ( ω t + φ ), { \ displaystyle E_ { d } = { \ frac { 1 } { 2 } } mv ( t ) ^ { 2 } = { \ frac { 1 } { 2 } } m \ omega ^ { 2 } A ^ { 2 } \ sin ^ { 2 } ( \ omega t + \ varphi ) = { \ frac { 1 } { 2 } } kA ^ { 2 } \ sin ^ { 2 } ( \ omega t + \ varphi ), }
Thế năng
E
t
{\displaystyle E_{t}\,}

E
t
=
1
2k
x
(
t)
2
=
1
2k
A
2
cos
2
(
ω
t
+
φ
)
.{\displaystyle E_{t}={\frac {1}{2}}kx(t)^{2}={\frac {1}{2}}kA^{2}\cos ^{2}(\omega t+\varphi ).}
Năng lượng toàn phần của hệ có giá trị không đổi :
- E = E d + E t = 1 2 k A 2 = c o n s t a n t. { \ displaystyle E = E_ { d } + E_ { t } = { \ frac { 1 } { 2 } } kA ^ { 2 } = constant. }
Source: https://mindovermetal.org
Category: Ứng dụng hay






























