Phương pháp đường chéo trong hóa học: Quy tắc, Sơ đồ và Bài tập

Quy tắc đường chéo là gì? Chuyên đề phương pháp đường chéo trong hóa học? Phương pháp đường chéo tỉ khối? Sơ đồ đường chéo tỉ khối?… Trong bài viết dưới đây, hãy cùng DINHNGHIA.VN đi tìm câu trả lời cho những thắc mắc trên nhé!

Quy tắc đường chéo là gì? Phương pháp đường chéo là gì?

Phương pháp đường chéo là chiêu thức thường được vận dụng cho những bài toán hỗn hợp chứa 2 thành phần mà nhu yếu của bài toán là xác lập tỉ lệ giữa 2 thành phần đó .

Đây là phương pháp có nhiều ưu điểm, giúp tăng tốc độ tính toán, và là 1 công cụ bổ trợ rất đắc lực cho phương pháp trung bình.

• Phương pháp đường chéo hoàn toàn có thể vận dụng tốt cho nhiều trường hợp, nhiều dạng bài tập, đặc biệt quan trọng là dạng bài pha chế dung dịch và tính thành phần hỗn hợp .
• Thường sử dụng tích hợp giữa đường chéo với giải pháp trung bình và chiêu thức bảo toàn nguyên tố. Với hỗn hợp phức tạp hoàn toàn có thể sử dụng tích hợp nhiều đường chéo .
• Trong đa phần trường hợp không thiết yếu phải viết sơ đồ dường chéo nhằm mục đích rút ngắn thời hạn làm bài .

Nhược điểm của chiêu thức này là không vận dụng được cho những bài toán trong đó có xảy ra phản ứng giữa những chất tan với nhau, không vận dụng được với trường hợp đo lường và thống kê pH .

Các bước giải bài toán bằng phương pháp đường chéo

• Xác định trị số cần tìm từ đề bài
• Chuyển những số liệu sang dạng đại lượng % khối lượng
• Xây dựng đường chéo \ ( \ rightarrow \ ) Kết quả bài toán .

Các dạng bài tập về phương pháp đường chéo

Dạng 1: Tính toán hàm lượng các đồng vị

• Đồng vị là các nguyên tử có cùng số proton nhưng khác nhau về số khối nên cùng thuộc một nguyên tố hóa học và có cùng vị trí trong bảng tuần hoàn các nguyên tố hóa học.
• Khác với số khối của đồng vị, khối lượng nguyên tử trung bình là giá trị trung bình những số khối của đồng vị tạo nên nguyên tố đó. Trong trường hợp nguyên tố được tạo nên bởi 2 đồng vị đa phần, ta hoàn toàn có thể thuận tiện tính được hàm lượng chất mỗi đồng vị bằng chiêu thức đường chéo .

Ví dụ 1: Nguyên tử khối trung bình của Br là 79,319. Br có 2 đồng vị bền: \(_{35}^{79}\textrm{Br}\) và \(_{35}^{81}\textrm{Br}\). Tính hàm lượng phần trăm mỗi đồng vị.

Cách giải:

Áp dụng giải pháp đường chéo, ta có :

Dạng 2: Tính tỷ lệ thành phần của hỗn hợp khí qua tỷ khối

Ví dụ 2: Tỉ khối hơi của \(N_{2}\) và \(H_{2}\) so vs \(O_{2}\) là 0,3125. Thành phần % thể tích của \(N_{2}\) trong hỗn hợp là bao nhiêu?

Cách giải:

Áp dụng giải pháp đường chéo ta có :

Vậy % thể tích của \ ( N_ { 2 } \ ) trong hỗn hợp trên là 44,44 %

Dạng 3: Tính toán trong pha chế các dung dịch có cùng chất tan

• Dung dịch 1 : Có khối lượng \ ( m_ { 1 } \ ), thể tích \ ( V_ { 1 } \ ), nồng độ \ ( C_ { 1 } \ ), khối lượng riêng \ ( d_ { 1 } \ )
• Dung dịch 2 : Có khối lượng \ ( m_ { 2 } \ ), thể tích \ ( V_ { 2 } \ ), nồng độ \ ( C_ { 2 } \ ) ( \ ( C_ { 2 } > C_ { 1 } \ ) ), khối lượng riêng \ ( d_ { 2 } \ )
• Dung dịch thu được : có khối lượng \ ( m = m_ { 1 } + m_ { 2 } \ ), thể tích \ ( V = V_ { 1 } + V_ { 2 } \ ) và khối lượng riêng d .

Sơ đồ đường chéo và công thức tương ứng với mỗi trường hợp là :

Ví dụ 3: Cần lấy bao nhiêu gam tinh thể \(CuSO_{4}.5H_{2}O\) và bao nhiêu gam dung dịch \(CuSO_{4}\) 8% để pha thành 280 gam dung dịch \(CuSO_{4}\) 16%

Cách giải:

Coi \ ( CuSO_ { 4 }. 5H _ { 2 } O \ ) là dung dịch \ ( CuSO_ { 4 } \ ) ta có :
C % = \ ( \ frac { 160 } { 250 }. 100 \ ) = 64 %
Áp dụng chiêu thức đường chéo, ta có :

Vậy cần lấy 40 gam \ ( CuSO_ { 4 }. 5H _ { 2 } O \ ) và 240 gam \ ( CuSO_ { 4 } \ ) để pha thành 280 gam dung dịch \ ( CuSO_ { 4 } \ ) 16 % .

Dạng 4: Tính thành phần hỗn hợp muối trong phản ứng giữa đơn bazơ với đa axit

Ví dụ 4: Thêm 250 ml dung dịch NaOH 2M vào 200 ml dung dịch \(H_{3}PO_{4}\) 1,5M. Muối tạo thành và khối lượng tương ứng là bao nhiêu?

Cách giải:

Ta có :
\ ( 1 < \ frac { n_ { NaOH } } { n_ { H_ { 3 } PO_ { 4 } } } = \ frac { 5 } { 3 } < 2 \ ) \ ( \ Rightarrow \ ) Tạo ra hỗn hợp 2 muối : \ ( NaH_ { 2 } PO_ { 4 }, Na_ { 2 } HPO_ { 4 } \ ) Sơ đồ đường chéo :

\ ( \ Rightarrow \ frac { n_ { Na_ { 2 } HPO_ { 4 } } } { n_ { NaH_ { 2 } PO_ { 4 } } } = \ frac { 2 } { 1 } \ Rightarrow n_ { Na_ { 2 } HPO_ { 4 } } = 2 n_ { NaH_ { 2 } PO_ { 4 } } \ )
Mà \ ( n_ { Na_ { 2 } HPO_ { 4 } } + n_ { NaH_ { 2 } PO_ { 4 } } = n_ { H_ { 3 } PO_ { 4 } } = 0,3 \, ( mol ) \ )

\(\Rightarrow \left\{\begin{matrix} n_{Na_{2}HPO_{4}} = 0,2\, (mol)\\ n_{NaH_{2}PO_{4}} = 0,1\, (mol) \end{matrix}\right. \Rightarrow \left\{\begin{matrix} m_{Na_{2}HPO_{4}} = 0,2.142 = 28,4\, (gam)\\ m_{NaH_{2}PO_{4}} = 0,1.120 = 12\, (gam) \end{matrix}\right.\)

Dạng 5: Tính tỷ lệ các chất trong hỗn hợp hai chất hữu cơ

Ví dụ 5: Đốt cháy hoàn toàn hỗn hợp 2 hiđrocacbon đồng đẳng liên tiếp, thu được 0,9 mol \(CO_{2}\) và 1,4 mol \(H_{2}O\). Thành phần % về thể tích của mỗi chất trong hỗn hợp ban đầu là bao nhiêu?

Cách giải:

Vì \ ( n_ { CO_ { 2 } } < n_ { H_ { 2 } O } \ ) suy ra hai hiđrocacbon đã cho là 2 ankan Gọi công thức phân tử trung bình của 2 ankan này là : \ ( C_ { \ bar { n } } H_ { 2 \ bar { n } + 2 } \ ) Từ giả thiết, ta có : \ ( \ frac { n_ { H_ { 2 } O } } { n_ { CO_ { 2 } } } = \ frac { \ bar { n } + 1 } { \ bar { n } } = \ frac { 1,4 } { 0,9 } \ Rightarrow \ bar { n } = 1,8 \ ) \ ( \ Rightarrow \ ) Hai ankan là \ ( CH_ { 4 } \ ) và \ ( C_ { 2 } H_ { 6 } \ ) Áp dụng giải pháp đường chéo, ta có :

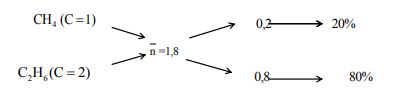
Vậy thành phần % về thể tích của \ ( CH_ { 4 } \ ) và \ ( C_ { 2 } H_ { 6 } \ ) lần lượt là 20 % và 80 % .

Dạng 6: Tính tỷ lệ các chất trong hỗn hợp 2 chất vô cơ

Ví dụ 6: Hòa tan 3,164 gam hỗn hợp 2 muối \(CaCO_{3}\) và \(BaCO_{3}\) bằng dung dịch HCl dư, thu được 448 ml khí \(BaCO_{3}\) (đktc). Thành phần % số mol của \(BaCO_{3}\) trong hỗn hợp là bao nhiêu?

Cách giải:

Ta có :
\ ( n_ { CO_ { 2 } } = \ frac { 0,448 } { 22,4 } = 0,02 \, ( mol ) \ Rightarrow \ bar { M } = \ frac { 3,164 } { 0,02 } = 158,2 \ )
Áp dụng sơ đồ đường chéo ta có :
bài tập nổi bật về giải pháp đường chéo

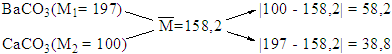
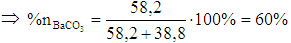
Vậy thành phần % số mol của \ ( BaCO_ { 3 } \ ) trong hỗn hợp là 60 %

Xem thêm >>> Dãy hoạt động hóa học của kim loại là gì? Ý nghĩa dãy hoạt động hóa học

Xem thêm >>> Phương pháp tăng giảm khối lượng: Nội dung và Các dạng bài tập 

Như vậy bài viết trên đây của DINHNGHIA.VN đã giúp bạn hệ thống lại kiến thức về phương pháp đường chéo. Hy vọng với những thông tin mà chúng tôi đã cung cấp bạn đã nắm được quy tắc đường chéo là gì, lý thuyết về chuyên đề phương pháp đường chéo trong hóa học cũng như trả lời được phương pháp đường chéo tỉ khối là gì. Chúc bạn luôn học tốt!

5
/
5
(
3
bầu chọn

)

Please follow and like us :

Source: https://mindovermetal.org
Category: Ứng dụng hay