Ứng dụng tích phân tính diện tích hình phẳng lớp 12

Ứng dụng tích phân tính diện tích hình phẳng là dạng toán quan trọng mà học sinh cần biết. Trong đề thi tham khảo toán của bộ GD&ĐT ra ngày 1/4/2021, có 2 câu thuộc dạng toán này. Nếu bạn đã có kiến thức căn bản về tích phân thì mời bạn xem bài viết ứng dụng tích phân ngay sau đây

1. Ứng dụng tích phân tính diện tích

Cho hàm số y = f ( x ) liên tục trên [ a ; b ]. Khi đó diện tích S của hình phẳng ( D ) số lượng giới hạn bởi : Đồ thị hàm số y = f ( x ) ; trục Ox : ( y = 0 ) và hai đường thẳng x = a ; x = b là : USD S = \ int \ limits_ { a } ^ { b } { \ left | f \ left ( x \ right ) \ right | dx } USD .

$\int\limits_{a}^{b}{\left| f\left( x \right) \right|dx}=\left| \int\limits_{a}^{b}{f\left( x \right)dx} \right|$ công thức này chỉ đúng khi f(x) không đổi dấu trên khoảng (a; b).

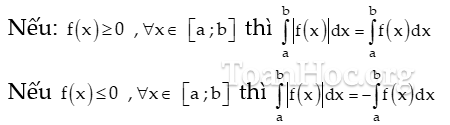
Chú ý: Nếu phương trình f(x) = 0 có k nghiệm phân biệt ${{x}_{1}},{{x}_{2}},…,{{x}_{k}}$ trên (a;b) thì trên mỗi khoảng $\left( a;{{x}_{1}} \right),\left( {{x}_{1}};{{x}_{2}} \right)…\left( {{x}_{k}};b \right)$ biểu thức f(x) không đổi dấu.

Khi đó tích phân USD S = \ int \ limits_ { a } ^ { b } { \ left | f \ left ( x \ right ) \ right | dx } USD được tính như sau :

Công thức tính diện tích hình phẳng giới hạn bởi các đường: $y=f\left( x \right)$ và $y=g\left( x \right)$và hai đường thẳng $x=a,x=b\left( a

2. Bài tập 

Bài tập 1. Một hình phẳng A được giới hạn bởi 3 đường y = lnx; x = e; và trục Ox. Hãy tìm diện tích hình phẳng A trên.

Lời giải
Diện tích cần tính là : USD { { S } _ { A } } = \ int \ limits_ { \ frac { 1 } { e } } ^ { e } { \ left | \ ln x \ right | dx } = \ int \ limits_ { 1 } ^ { e } { \ ln xdx } – \ int \ limits_ { \ frac { 1 } { e } } ^ { 1 } { \ ln xdx } USD
Mà USD \ ln x = x ( \ ln x ) ’ + x ’ \ ln x = ( x \ ln x ) ’ USD
Nên USD { { S } _ { A } } = \ left. x \ ln x \ right | _ { 1 } ^ { e } – \ left. x \ ln x \ right | _ { \ frac { 1 } { e } } ^ { 1 } = e – \ frac { 1 } { e } USD ( đvdt ) .

Kết luận: Diện tích hình phẳng A cần tìm là ${{S}_{A}}=e-\frac{1}{e}$(đvdt).

Bài tập 2 ( trích câu 44 trong đề tham khảo 2021). Ông Bình làm lan can ban công ngôi nhà của mình bằng một tấm kính cường lực. Tấm kính đó là một phần của mặt xung quanh của một hình trụ như hình bên. Biết giá tiền của kính như trên là 1. 500. 000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bình mua tấm kính trên là bao nhiêu?

A. 23.591.000 đồng .
B. 36.173.000 đồng .
C. 9.437.000 đồng .
D. 4.718.000 đồng .
Lời giải
Chọn câu C
Gọi USD r USD là nửa đường kính đáy của hình tròn trụ thì ta có USD 4,45 = 2 r \ cdot \ sin 150 { } ^ \ circ \ Rightarrow r = 4,45. USD Từ đó suy ra góc ở tâm ứng với cung này là USD 60 { } ^ \ circ USD và cung này bằng USD \ frac { 1 } { 6 } USD chu vi đường tròn đáy
Ta có diện tích xung quanh của những hình tròn trụ là USD { { S } _ { xd } } = 2 \ pi rh USD nên diện tích của tấm kính chính là USD \ frac { 1 } { 6 } \ cdot 2 \ pi rh = \ frac { \ pi rh } { 3 }. USD Do đó, giá tiền là USD 1.500.000 \ times \ frac { \ pi \ cdot 4,45 \ cdot 1,35 } { 3 } \ approx 9.437.000 USD đồng

Bài tập 3 ( trích câu 48 trong đề tham khảo 2021). Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình bên. Biết hàm số f(x) đạt cực trị tại hai điểm ${{x}_{1}},{{x}_{2}}$ thỏa mãn ${{x}_{2}}={{x}_{1}}+2$ và $f\left( {{x}_{1}} \right)+f\left( {{x}_{2}} \right)=0$. Gọi ${{S}_{1}}$ và ${{S}_{2}}$ là diện tích của hai hinh phẳng được gạch trong hình bên. Tì số $\frac{{{S}_{1}}}{{{S}_{2}}}$ bằng

A. USD \ frac { 3 } { 4 } USD .

B.$\frac{5}{8}$.

C. USD \ frac { 3 } { 8 } USD .
D. USD \ frac { 3 } { 5 } USD .
Lời giải
Chọn câu D
Rõ ràng hiệu quả bài toán không đổi nếu ta tịnh tiến đồ thị sang trái cho điểm uốn trùng gốc tọa độ O. Gọi USD g ( x ) = a { { x } ^ { 3 } } + b { { x } ^ { 2 } } + cx + d USD là hàm số khi đó thì dễ thấy USD g ( x ) USD lẻ nên có ngay USD b = d = 0 USD và USD g ( x ) = a { { x } ^ { 3 } } + cx USD có hai điểm cực trị tương ứng là USD – 1,1, USD cũng là nghiệm của USD 3 a { { x } ^ { 2 } } + c = 0. USD Từ đó thuận tiện có USD g ( x ) = k ( { { x } ^ { 3 } } – 3 x ) USD với USD k > 0. USD
Xét diện tích hình chữ nhật USD { { S } _ { 1 } } + { { S } _ { 2 } } = \ left | ( – 1 ) \ cdot g ( – 1 ) \ right | = 2 k. USD Ngoài ra ,
USD { { S } _ { 2 } } = k \ int_ { – 1 } ^ { 0 } { \ left | { { x } ^ { 3 } } – 3 x \ right | \ text { d } x } = \ frac { 5 } { 4 } k. USD
Vì thế USD { { S } _ { 1 } } = 2 k – \ frac { 5 k } { 4 } = \ frac { 3 k } { 4 } USD và USD \ frac { { { S } _ { 1 } } } { { { S } _ { 2 } } } = \ frac { 3 } { 5 }. USD

Bài tập 4. Cho parabol (P): $y=-{{x}^{2}}+2x$, có đỉnh S và A là giao điểm khác O của (P) và trục hoành. M là điểm di động trên SA, tiếp tuyến của (P) tại M cắt Ox, Oy tại E, F. Tìm giá trị nhỏ nhất của tổng diện tích 2 tam giác cong MOE và MAF.

Lời giải
Tiếp tuyến tại USD M \ left ( m ; 2 m – { { m } ^ { 2 } } \ right ), \ mathsf { } 1 \ le m \ le 2 USD có phương trình : USD y = \ left ( 2-2 m \ right ) \ left ( x-m \ right ) + 2 m – { { m } ^ { 2 } } \ Leftrightarrow y = \ left ( 2-2 m \ right ) x + { { m } ^ { 2 } } USD

Ta có: $E\left( 0;{{m}^{2}} \right);\mathsf{ }F\left( \frac{{{m}^{2}}}{2m-2};0 \right)$ với $1
Gọi S là diện tích hình phẳng số lượng giới hạn bởi ( P ) và trục hoành : USD S = \ int \ limits_ { 0 } ^ { 2 } { \ left | – { { x } ^ { 2 } } + 2 x \ right | dx = \ frac { 4 } { 3 } } USD .

Ta thấy, USD { { S } _ { MOE } } + { { S } _ { MAF } } = { { S } _ { OEF } } – S, USD USD \ left ( { { S } _ { MOE } } + { { S } _ { MAF } } \ right ) \ min \ Leftrightarrow \ left ( { { S } _ { OEF } } \ right ) \ min USD
USD \ left ( { { S } _ { MOE } } + { { S } _ { MAF } } \ right ) \ min = { { \ left ( \ frac { 4 } { 3 } \ right ) } ^ { 3 } } – \ frac { 4 } { 3 } = \ frac { 28 } { 27 } USD khi USD m = \ frac { 4 } { 3 } USD .
Vậy, USD m = \ frac { 4 } { 3 } USD thỏa bài toán

Bài tập 5. Tìm m để đồ thị (C): $y={{x}^{4}}-2m{{x}^{2}}+m+2$ cắt Ox tại bốn điểm phân biệt và diện tích hình phẳng nằm trên Ox giới hạn bởi (C) và Ox bằng diện tích hình phẳng phía dưới trục Ox giới hạn bởi (C) và Ox.

Lời giải .
Phương trình hoành độ giao điểm của ( C ) và ( C ) : USD { { x } ^ { 4 } } – 2 m { { x } ^ { 2 } } + m + 2 = 0 \ left ( 1 \ right ) USD
Đặt USD t = { { x } ^ { 2 } }, \ text { } t \ ge 0 USD, ta có phương trình : USD { { t } ^ { 2 } } – 2 mt + m + 2 = 0 \ mathsf { } \ left ( 2 \ right ) USD .
Yêu cầu bài toán < => ( 2 ) có hai nghiệm t > 0 phân biệt

Gọi USD { { t } _ { 1 } }, { { t } _ { 2 } } \ text { ( } 0 < { { t } _ { 1 } } < { { t } _ { 2 } } ) USD là hai nghiệm của ( 2 ). Khi đó ( 1 ) có bốn nghiệm theo thứ tự tăng dần là : USD { { x } _ { 1 } } = - \ sqrt { { { t } _ { 2 } } } ; { { x } _ { 2 } } = - \ sqrt { { { t } _ { 1 } } } ; { { x } _ { 3 } } = \ sqrt { { { t } _ { 1 } } } ; { { x } _ { 4 } } = \ sqrt { { { t } _ { 2 } } } USD . Do tính đối xứng của ( C ) nên nhu yếu bài toán

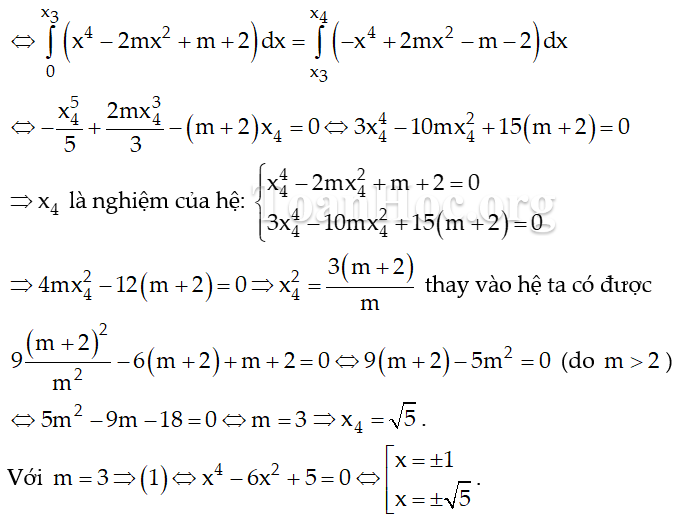
Vậy m = 3 là giá trị cần tìm.

Trên đây là bài viết chia sẻ ứng dụng tích phân tính diện tích hình phẳng của toán lớp 12. Hy vọng bài viết này hữu ích với bạn. Chúc bạn học hiệu quả.

Source: https://mindovermetal.org
Category: Ứng dụng hay