Lý thuyết ứng dụng tích phân trong hình học>

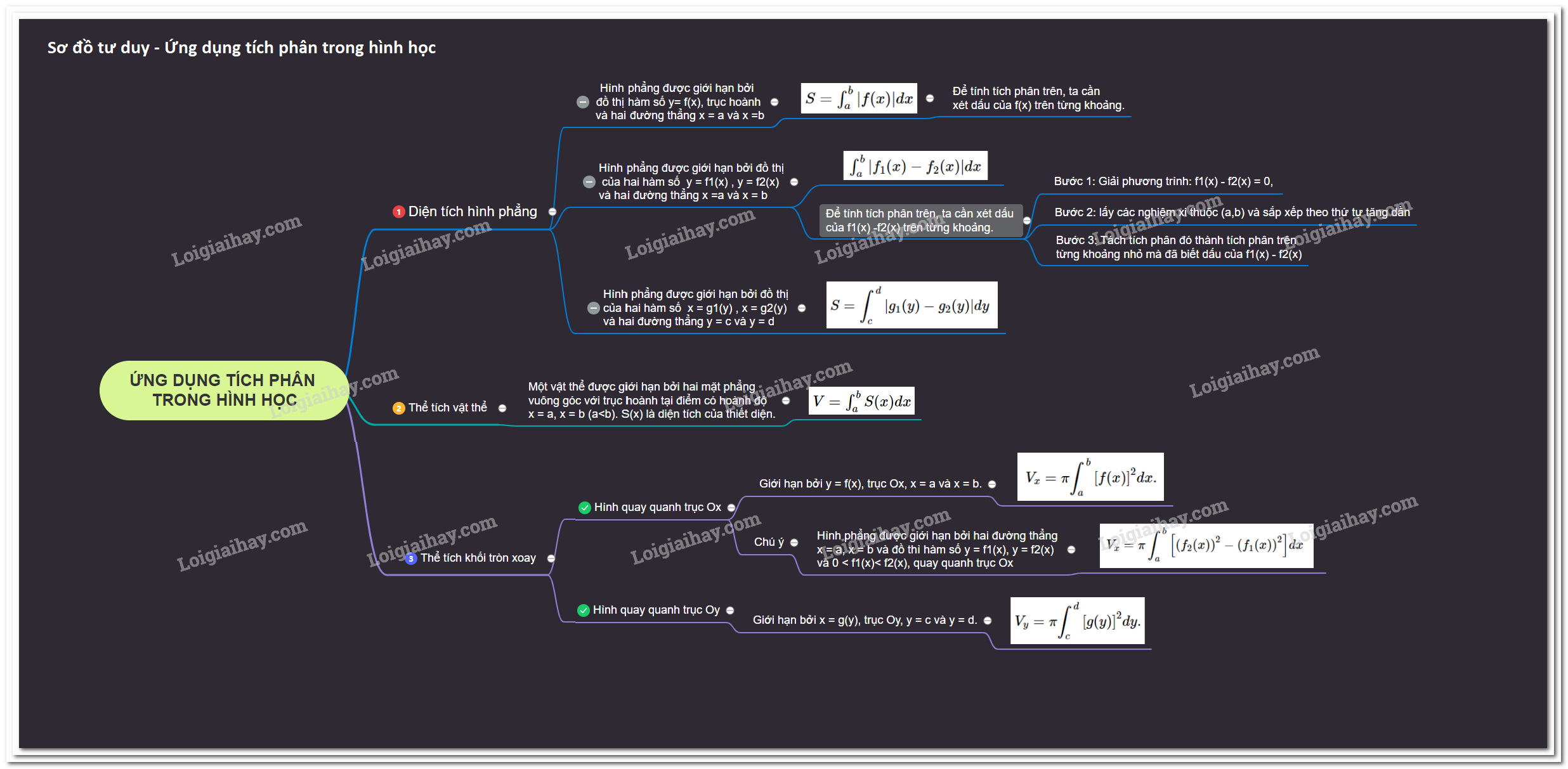
1. Tính diện tích hình phẳng

a ) Nếu hình phẳng được số lượng giới hạn bởi đồ thị hàm số \ ( y = f ( x ) \ ) liên tục trên đoạn \ ( [ a ; b ] \ ) ; trục hoành và hai đường thẳng \ ( x = a ; x = b \ ), thì diện tích quy hoạnh \ ( S \ ) được cho bởi công thức :\ ( S = \ int_a ^ b { \ left | { f ( x ) } \ right | } dx \ ) ( 1 )

Chú ý: Để tính tích phân trên, ta xét dấu của \(f(x)\) trên đoạn \([a,b]\). Nếu \(f(x)\) không đổi dấu trên khoảng \((c;d) ⊂ [a;b]\) thì :

\ ( \ int_c ^ d { \ left | { f ( x ) } \ right | } dx = \ left | { \ int_c ^ d f ( x ) dx } \ right | \ )Chẳng hạn ta có :\ ( \ int_a ^ b { \ left | { f ( x ) } \ right | } dx = \ left | { \ int_a ^ { { c_1 } } f ( x ) dx } \ right | + \ left | { \ int_ { { c_1 } } ^ { { c_2 } } f ( x ) dx } \ right | \ ) \ ( + \ left | { \ int_ { { c_2 } } ^ { { c_3 } } f ( x ) dx } \ right | + \ left | { \ int_ { { c_3 } } ^ b f ( x ) dx } \ right | \ )b ) Nếu hình phẳng được số lượng giới hạn bởi đồ thị của hai hàm số \ ( y = { \ rm { } } { f_1 } \ left ( x \ right ) \ ) và \ ( y = { \ rm { } } { f_2 } \ left ( x \ right ) \ ) liên tục trên đoạn [ a ; b ] và hai đường thẳng \ ( x = a, x = b \ ) thì diện tích quy hoạnh \ ( S \ ) được cho bởi công thức :\ ( \ int_a ^ b { \ left | { { f_1 } ( x ) – { f_2 } ( x ) } \ right | } dx \ ) ( 2 )

Chú ý: Để tính tích phân trên, ta xét dấu \(f\left( x \right) = \;{f_1}\left( x \right){\rm{ }}\; – {\rm{ }}{f_2}\left( x \right)\) trên đoạn \([a;b]\) hoặc tìm nghiệm của nó trên khoảng \((a;b)\), sau đó áp dụng tính chất nêu ở chú ý trên. Cụ thể ta thực hiện các bước sau:

Bước 1 : Giải phương trình : \ ( { f_1 } \ left ( x \ right ) { \ rm { } } \ ; – { \ rm { } } { f_2 } \ left ( x \ right ) { \ rm { } } = { \ rm { } } 0 \ ), tìm những nghiệm \ ( { x_i } \ ; \ in { \ rm { } } \ left ( { a ; b } \ right ) \ )Bước 2 : Sắp xếp những nghiệm theo thứ tự tăng dần, ví dụ điển hình có n nghiệm :\ [ { x_ { 1 \ ; } } < { \ rm { } } { x_2 } \ ; < { \ rm { } } \ ldots { \ rm { } } < { \ rm { } } { x_ { n. } } \ ]

\(S = \int_a {^b} \left| {f(x)} \right|dx = \left| {\int_a^{{x_1}} f (x)dx} \right| + \left| {\int_{{x_1}}^{{x_2}} f (x)dx} \right| + … + \left| {\int_{{x_n}}^b f (x)dx} \right|\)

Nếu hình phẳng nói trên không cho số lượng giới hạn bởi hai đường thẳng \ ( x = a, x = b \ ) thì ta tìm những nghiệm trên tập xác lập và trong công thức ( * ), a được sửa chữa thay thế bởi \ ( { x_1 } \ ), b được thay thế sửa chữa bởi \ ( { x_n } \ ) .Công thức ( 1 ) là trường hợp đặc biệt quan trọng của công thức ( 2 ) khi \ ( y { \ rm { } } = { \ rm { } } { f_1 } \ left ( x \ right ) = { \ rm { } } 0 \ ) hoặc \ ( y { \ rm { } } = { \ rm { } } { f_2 } \ left ( x \ right ) { \ rm { = } } 0 \ )Tương tự, hình phẳng được số lượng giới hạn bởi đồ thị hàm số \ ( \ ; x { \ rm { } } = { \ rm { } } { g_1 } \ left ( y \ right ), \ ; x { \ rm { } } = { \ rm { } } { g_2 } \ left ( y \ right ) \ ) liên tục trên đoạn \ ( [ c ; d ] \ ) và hai đường thẳng \ ( y = c, y = d \ ) có diện tích quy hoạnh được cho bởi công thức : USD USD S = \ int_c ^ d { \ left | { { g_1 } ( y ) – { g_2 } ( y ) } \ right | } dy USD USD

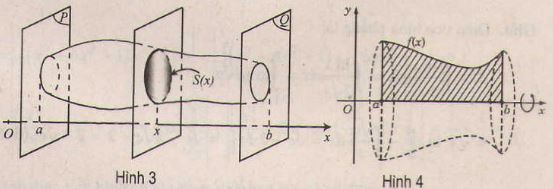
2. Thể tích vật thể

Một vật thể được giới hạn bởi hai mặt phẳng vuông góc với trục hoành tại điểm có hoành độ \(x = a, x = b (a

3. Thể tích khối tròn xoay

a ) Hình phẳng quay quanh trục \ ( Ox \ ) : Cho hình phẳng được số lượng giới hạn bởi đồ thị hàm số \ ( y = f ( x ) \ ) không âm và liên tục trên đoạn \ ( [ a ; b ] \ ), trục \ ( Ox \ ) và hai đường thẳng \ ( x = a, x = b \ ) quay quanh trục \ ( Ox \ ), ta được khối tròn xoay ( h. 4 ). Thể tích \ ( { V_x } \ ) của khối tròn xoay này được cho bởi công thức : USD USD { V_x } = \ pi { \ int_a ^ b { \ left [ { f ( x ) } \ right ] } ^ 2 } dx. USD USDb ) Hình phẳng quay quanh trục \ ( Oy \ ) ( kiến thức và kỹ năng bổ trợ ) : Cho hình phẳng được số lượng giới hạn bởi đồ thị hàm số \ ( x = g ( y ) \ ) không âm và liên tục trên đoạn \ ( [ c ; d ] \ ), trục \ ( Oy \ ) và hai đường thẳng \ ( y = c, y = d \ ) quay quanh trục \ ( Oy \ ), ta được khối tròn xoay. Thể tích Vy của khối tròn xoay này được cho bởi công thức : USD USD { V_y } = \ pi { \ int_c ^ d { \ left [ { g ( y ) } \ right ] } ^ 2 } dy. USD USD

Chú ý. Thể tích của vật thể tạo bởi hình phẳng được giới hạn bởi hai đường thẳng \(x = a\), \(x = b\) và đồ thị hàm số \(y{\rm{ }} = {\rm{ }}{f_1}\left( x \right),{\rm{ }}y{\rm{ }} = {\rm{ }}{f_2}\left( x \right)\) liên tục và \(0\; \le \;\;{f_1}\left( x \right)\; \le {\rm{ }}{f_2}\left( x \right)\) trên đoạn \([a;b]\) quay quanh trục \(Ox\) được cho bởi công thức: $${V_x} = \pi \int_a^b {\left[ {{{({f_2}(x))}^2} – {{({f_1}(x))}^2}} \right]} dx$$

Tương tự, đổi vai trò \ ( x \ ) và \ ( y \ ) cho nhau, ta có công thức tính \ ( { V_y } \ ) ( khi hình phẳng quay quanh trục \ ( Oy \ ) ) .

Loigiaihay.com

Source: https://mindovermetal.org
Category: Ứng dụng hay