Tích vô hướng của hai vectơ là chuyên đề hình học thuộc chương 2 của chương trình hình học lớp 10. Đây là một chuyên đề được đánh giá là khá dễ. Tuy nhiên số lượng tài liệu nói toàn bộ vấn đề lý thuyết cũng như bài tập của chuyên đề dường như là không có. Hãy cùng chúng tôi tìm hiểu chuyên đề này ngay bên dưới đây nhé.
TẢI XUỐNG PDF ↓
Mục lục nội dung
Nhắc lại kiến thức
Giá trị lượng giác của góc bất kỳ :
Bạn đang đọc: Bài tập và lý thuyết chi tiết
Định nghĩa
Với mỗi góc \ [ \ alpha ( { { 0 } ^ { 0 } } \ le \ alpha \ le { { 180 } ^ { 0 } } ) \ ] ta xác lập một điểm \ [ M \ ] trên nửa đường tròn đơn vị chức năng sao cho góc \ [ \ widehat { xOM } = \ alpha \ ] và giả sử điểm \ [ M \ ] có tọa độ \ [ M ( { { x } _ { 0 } } ; { { y } _ { 0 } } ) \ ] .
Khi đó ta có định nghĩa :
\ [ Sin \ ] của góc \ [ \ alpha \ ] là \ [ { { y } _ { 0 } } \ ], kí hiệu là \ [ \ sin \ alpha = { { y } _ { 0 } } \ ] .
\ [ cosin \ ] của góc \ [ \ alpha \ ] là \ [ { { x } _ { 0 } } \ ], kí hiệu là \ [ cos \ alpha = { { x } _ { 0 } } \ ] .
\ [ tang \ ] của góc \ [ \ alpha \ ] là \ [ ( { { x } _ { 0 } } \ ne 0 ) \ ], ký hiệu \ [ tan \ alpha = \ frac { { { x } _ { 0 } } } { { { y } _ { 0 } } } \ ] .
\ [ cotang \ ] cuả góc \ [ \ alpha \ ] là \ [ ( { { y } _ { 0 } } \ ne 0 ) \ ], ký hiệu \ [ cot \ alpha = \ frac { { { y } _ { 0 } } } { { { x } _ { 0 } } } \ ] .
Các số \ [ \ sin \ alpha, cos \ alpha, tan \ alpha, cot \ alpha \ ] được gọi là những giá trị lượng giác của góc \ [ \ alpha \ ]
Tính chất
Sự liên hệ giữa những giá trị lượng giác của những góc bù nhau
\ [ sin \ alpha = sin ( { { 180 } ^ { 0 } } \ alpha ) \ ]
\ [ cos \ alpha = – cos ( ( { { 180 } ^ { 0 } } \ alpha ) \ ]
\ [ tan \ alpha = tan ( { { 180 } ^ { 0 } } \ alpha ) \ ]
\ [ cot \ alpha = – cot ( { { 180 } ^ { 0 } } \ alpha ) \ ]
Hai góc bù nhau thì có sin bằng nhau còn cos, tan, cot thì đối nhau
Bảng giá trị lượng giác của các góc đặc biệt: (SGK) Xem ở chương tích vô hướng của hai vecto
Định nghĩa : Cho hai vectơ \ [ \ overrightarrow { a } \ ] và \ [ { \ vec { b } } \ ] đều khác vectơ \ [ 0 \ ]. Từ một điểm \ [ 0 \ ] bât kỳ ta vẽ \ [ \ overrightarrow { a } \ ] và \ [ { \ vec { b } } \ ] → đều khác vec tơ \ [ 0 \ ]. Từ một điểm \ [ O \ ] bất kể ta vẽ \ [ \ overrightarrow { OA } = \ overrightarrow { a } \ ] và \ [ \ overrightarrow { OB } = \ vec { b } \ ] .
góc \ [ \ widehat { AOB } \ ] với số đo từ \ [ { { 0 } ^ { 0 } } \ ] đến \ [ { { 180 } ^ { 0 } } \ ] độ được gọi là góc giữa hai vectơ \ [ { \ vec { a } } \ ] và \ [ { \ vec { b } } \ ] .
Người ta ký hiệu góc giữa hai vectơ \ [ { \ vec { a } } \ ] và \ [ { \ vec { b } } \ ] là \ [ \ left ( \ vec { a } ; \ vec { b } \ right ) \ ] Nếu
\ [ ( \ vec { a } ; \ vec { b } ) = { { 90 } ^ { 0 } } \ ] thì ta nói rằng \ [ { \ vec { a } } \ ] và \ [ { \ vec { b } } \ ] vuông góc với nhau. Ký hiệu là \ [ \ vec { a } \ bot \ vec { b } \ ] hoặc \ [ \ vec { b } \ bot \ vec { a } \ ] .
Lý thuyết tích vô hướng của hai vecto :
Định nghĩa
Cho hai vectơ \ [ { \ vec { a } } \ ] và \ [ { \ vec { b } } \ ] khác vectơ \ [ { \ vec { 0 } } \ ]. Tích vô hướng của \ [ { \ vec { a } } \ ] và \ [ { \ vec { b } } \ ] là 1 số ít được ký hiệu là \ [ \ vec { a }. \ vec { b } \ ], được xác lập bởi công thức sau :
\ [ \ vec { a }. \ vec { b } = | \ vec { a } |. | \ vec { b } | cos ( \ vec { a }, \ vec { b } ) \ ]
Các tính chất của tích vô hướng
Người ta chứng tỏ được những đặc thù sau đây của tích vô hướng :
Với ba vectơ \ [ \ vec { a }, \ vec { b }, \ vec { c } \ ] bất kể và mọi số \ [ k \ ] ta có :
\ [ \ vec { a }. \ vec { b } = \ vec { b }. \ vec { a } \ ] ( đặc thù giao hoán )
\ [ \ vec { a }. ( \ vec { b } + \ vec { c } ) = \ vec { a }. \ vec { b } + \ vec { a }. \ vec { c } \ ] ( đặc thù phân phối )
\ [ ( k. \ vec { a } ). \ vec { b } = k. ( \ vec { a }. \ vec { b } ) = \ vec { a }. ( k. \ vec { b } ) \ ]
Biểu thức tọa độ của tích vô hướng
Trên mặt phẳng tọa độ \ [ ( 0 ; \ vec { i } ; \ vec { j } ) \ ], cho hai vec tơ \ [ \ vec { a } = ( { { a } _ { 1 } } ; { { a } _ { 2 } } ) \ ], \ [ \ vec { b } = ( { { b } _ { 1 } } ; { { b } _ { 2 } } ) \ ]. Khi đó tích vô hướng \ [ { \ vec { a } } \ ] và \ [ { \ vec { b } } \ ] là :
\ [ \ vec { a }. \ vec { b } = { { a } _ { 1 } } { { b } _ { 1 } } + { { a } _ { 2 } } { { b } _ { 2 } } \ ]
Nhận xét: Hai vectơ \[\vec{a}=({{a}_{1}};{{a}_{2}})\], \[\vec{b}=({{b}_{1}};{{b}_{2}})\] khác vectơ\[{\vec{0}}\]→ vuông góc với nhau khi và chỉ khi:
\ [ { { a } _ { 1 } } { { b } _ { 1 } } + { { a } _ { 2 } } { { b } _ { 2 } } = 0 \ ]
Ứng dụng
a ) Độ dài của vectơ : Độ dài của vec tơ \ [ \ vec { a } = ( { { a } _ { 1 } } ; { { a } _ { 2 } } ) \ ] được tính theo công thức :
\ [ \ vec { a } = \ sqrt { a_ { 1 } ^ { 2 } + a_ { 2 } ^ { 2 } } \ ]
b ) Góc giữa hai vec tơ : Từ định nghĩa tích vô hướng của hai vec tơ ta suy ra nếu \ [ \ vec { a } = ( { { a } _ { 1 } } ; { { a } _ { 2 } } ) \ ], \ [ \ vec { b } = ( { { b } _ { 1 } } ; { { b } _ { 2 } } ) \ ] khác vectơ \ [ { \ vec { 0 } } \ ] → thì ta có :
\ [ \ cos ( \ vec { a }, \ vec { b } ) = \ frac { \ vec { a }. \ vec { b } } { | \ overrightarrow { a |. | \ vec { b } } | } = \ frac { { { a } _ { 1 } }. { { b } _ { 1 } } + { { a } _ { 2 } }. { { b } _ { 2 } } } { \ sqrt { { { a } _ { 1 } } ^ { 2 } + { { a } _ { 2 } } ^ { 2 } }. \ sqrt { { { b } _ { 1 } } ^ { 2 } + { { b } _ { 2 } } ^ { 2 } } } \ ]
c ) Khoảng cách giữa hai điểm : Khoảng cách giữa hai điểm \ [ A ( { { x } _ { A } } ; { { y } _ { A } } ), B ( { { x } _ { B } } ; { { y } _ { B } } ) \ ] được tính theo công thức :
\ [ AB = \ sqrt { { { ( { { x } _ { B } } – { { x } _ { A } } ) } ^ { 2 } } + { { ( { { y } _ { B } } – { { y } _ { A } } ) } ^ { 2 } } } \ ]
Lý thuyết những hệ thức lượng trong tam giác và giải tam giác :
Nhắc lại hệ thức lượng trong tam giác vuông .
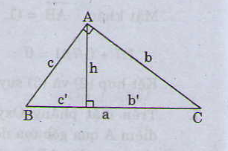
Cho tam giác \ [ ABC \ ] vuông góc tại đỉnh \ [ A ( \ hat { A } = { { 90 } ^ { 0 } } ) \ ], ta có :
1. \ [ { { b } ^ { 2 } } = ab \ prime ; { { c } ^ { 2 } } = a. c \ prime \ ] .
2. Định lý Pitago : \ [ { { a } ^ { 2 } } = { { b } ^ { 2 } } + { { c } ^ { 2 } } \ ] .
3. \ [ a. h = b. c \ ] .
4. \ [ { { h } ^ { 2 } } = b \ prime. c \ prime \ ] .
5. \ [ \ frac { 1 } { { { h } ^ { 2 } } } = \ frac { 1 } { { { b } ^ { 2 } } } + \ frac { 1 } { { { c } ^ { 2 } } } \ ] .
Định lý cosin
Định lí : Trong một tam giác bất kể, bình phương một cạnh bằng tổng những bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với \ [ cosin \ ] của góc xen giữa chúng .
Ta có những hệ thức sau :
\ [ { { a } ^ { 2 } } = { { b } ^ { 2 } } + { { c } ^ { 2 } } – 2 bc. cosA ( 1 ) \ ]
\ [ { { b } ^ { 2 } } = { { a } ^ { 2 } } + { { c } ^ { 2 } } – 2 accosB ( 2 ) \ ]
\[{{c}^{2}}={{a}^{2}}+{{b}^{2}}-2bccosC(3)\]
Xem thêm: Ứng dụng của tích phân tính diện tích, thể tích, quãng đường, vận tốc cực hay – Toán lớp 12
\ [ \ cos A = \ frac { { { b } ^ { 2 } } + { { c } ^ { 2 } } – { { a } ^ { 2 } } } { 2 bc } \ ]
\ [ \ cos B = \ frac { { { a } ^ { 2 } } + { { c } ^ { 2 } } – { { b } ^ { 2 } } } { 2 ac } \ ]
\ [ \ cos C = \ frac { { { a } ^ { 2 } } + { { b } ^ { 2 } } – { { c } ^ { 2 } } } { 2 ab } \ ]
Áp dụng : Tính độ dài đường trung tuyến của tam giác :
Cho tam giác \ [ ABC \ ] có những cạnh \ [ BC = a, CA = b \ ] và \ [ AB = c \ ]. Gọi \ [ { { m } _ { a } }, { { m } _ { b } } \ ] và \ [ { { m } _ { c } } \ ] là độ dài những đường trung tuyến lần lượt vẽ từ những đỉnh \ [ A, B, C \ ] của tam giác. Ta có
\ [ { { m } _ { a } } ^ { 2 } = \ frac { 2. ( { { b } ^ { 2 } } + { { c } ^ { 2 } } ) – { { a } ^ { 2 } } } { 4 } \ ]
\ [ { { m } _ { b } } ^ { 2 } = \ frac { 2. ( { { a } ^ { 2 } } + { { c } ^ { 2 } } ) – { { b } ^ { 2 } } } { 4 } \ ]
\ [ { { m } _ { c } } ^ { 2 } = \ frac { 2. ( { { a } ^ { 2 } } + { { b } ^ { 2 } } ) – { { c } ^ { 2 } } } { 4 } \ ]
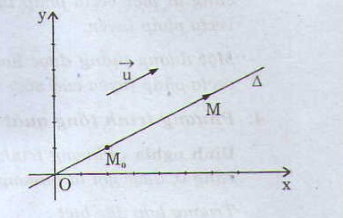
Định lí sin
Định lí : Trong tam giác \ [ ABC \ ] bất kể, tỉ số giữa một cạnh và sin của góc đối lập với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là :
\ [ \ frac { a } { sinA } = \ frac { b } { sinB } = \ frac { c } { sinC } = 2R \ ]
với \ [ R \ ] là nửa đường kính đường tròn ngoại tiếp tam giác
Công thức tính diện tích quy hoạnh tam giác :
Ta kí hiệu ha, hb và hc là những đường cao của tam giác \ [ ABC \ ] lần lượt vẽ từ những đình \ [ A, B, C \ ] và \ [ S \ ] là diện tích quy hoạnh tam giác đó .
Diện tích \ [ S \ ] của tam giác \ [ ABC \ ] được tính theo một trong những công thức sau
\ [ S = \ frac { 1 } { 2 } ab \ sin C = \ frac { 1 } { 2 } bc \ sin A = \ frac { 1 } { 2 } ca \ sin B \ ] ( 1 )
\ [ S = \ frac { abc } { 4R } \ ] ( 2 )
\ [ S = pr \ ] ( 3 )
\ [ S = \ sqrt { p ( p-a ) ( p-b ) ( p-c ) } \ ] ( công thức Hê – rông ) ( 4 )
Giải tam giác và ứng dụng vào việc đo đạc
Giải tam giác : Giải tam giác là tìm 1 số ít yếu tố của tam giác khi đã biết những yếu tố khác của tam giác đó .
Muốn giải tam giác ta cần tìm mối liên hệ giữa những yếu tố đã cho với những yếu tố chưa biết của tam giác trải qua những hệ thức đã được nêu trong định lí cosin, định lí sin và những công thức tính diện tích quy hoạnh tam giác .
Các bài toán về giải tam giác: Có 3 bài toán cơ bản về gỉải tam giác:
a) Giải tam giác khi biết một cạnh và hai góc.
Đối với bài toán này ta sử dụng định lí sin để tính cạnh còn lại
b) Giải tam giác khi biết hai cạnh và góc xen giữa
Đối với bài toán này ta sử dụng định lí cosin để tính cạnh thứ ba
c) Giải tam giác khi biết ba cạnh
Đối với bài toán này ta sử dụng định lí cosin để tính góc
\ [ \ cos A = \ frac { { { b } ^ { 2 } } + { { c } ^ { 2 } } – { { a } ^ { 2 } } } { 2 bc } \ ]
\ [ \ cos B = \ frac { { { a } ^ { 2 } } + { { c } ^ { 2 } } – { { b } ^ { 2 } } } { 2 ac } \ ]
\ [ cosC = \ frac { { { a } ^ { 2 } } + { { b } ^ { 2 } } – { { c } ^ { 2 } } } { 2 ab } \ ]
Chú ý:
1. Cần chú ý quan tâm là một tam giác giải được khi ta biết 3 yếu tố của nó, trong đó phải có tối thiểu một yếu tố độ dài ( tức là yếu tố góc không được quá 2 )
2. Việc giải tam giác được sử dụng vào những bài toán thực tiễn, nhất là những bài toán đo đạc
Bài tập tích vô hướng của hai vectơ
Vấn đề 1. Giá trị lượng giác của một góc bất kì
Dạng 1. Góc và dấu của những giá trị lượng giác
Dạng 2. Cho một giá trị lượng giác, tính những giá trị lượng giác còn lại
Dạng 3. Chứng minh, rút gọn một biểu thức
Vấn đề 2. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ
Dạng 1. Tính tích vô hướng của hai vectơ. Góc giữa hai vectơ
Dạng 2. Tính độ dài của một đoạn thẳng
Dạng 3. Chứng minh vuông góc
Dạng 4. Chứng minh một đẳng thức về tích vô hướng hay độ dài
Dạng 5. Tập hợp điểm – Cực trị
Dạng 6. Biểu thức tọa độ
Dạng 7. Tìm những điểm đặc biệt quan trọng trong tam giác
Dạng 8. Một số dạng toán thường gặp trên tam giác, tứ giác
Dạng 9. Tìm GTLN, GTNN trong hình học
Vấn đề 3. Hệ thức lượng trong tam giác
Dạng 1. Tính toán những đại lượng
Dạng 2. Chứng minh hệ thức
Dạng 3. Dạng tam giác
Xem thêm: Viber
Dạng 4. Giải tam giác và ứng dụng thực tiễn
Trên đây là toàn bộ các câu hỏi và bài tập về chủ đề tích vô hướng của hai vectơ. Mong rằng sẽ giúp các em chinh phục một phần nào chuyên đề này.
Để xem thêm nhiều tài liệu hay hơn nữa về chuyên đề Véctơ, những em chọn những mục ở cuối bài viết này để xem cụ thể hơn .
Source: https://mindovermetal.org
Category: Ứng dụng hay









