Lý thuyết trò chơi – Wikipedia tiếng Việt

Lý thuyết trò chơi, hoặc gọi đối sách luận, lí luận ván cờ, là một phân nhánh mới của toán học hiện đại, cũng là một môn học trọng yếu của vận trù học,[1] tác phẩm “Lí thuyết trò chơi và hành vi kinh tế” do John von Neumann viết chung với Oskar Morgenstern vào năm 1944, đã đánh dấu sự hình thành sơ bộ của hệ thống lí thuyết trò chơi hiện đại, do đó ông được gọi là “cha đẻ của lí thuyết trò chơi”.

Lí thuyết trò chơi hầu hết điều tra và nghiên cứu công dụng tương hỗ giữa những cấu trúc phấn khích đã được công thức hoá, là lí luận và giải pháp toán học để nghiên cứu và điều tra hiện tượng kỳ lạ có sẵn đặc thù đấu tranh hoặc cạnh tranh đối đầu. Lí thuyết trò chơi đắn đo Để ý đến hành vi dự liệu và hành vi thực tiễn, đồng thời điều tra và nghiên cứu sách lược ưu hoá của chúng. Các nhà sinh vật học sử dụng lí thuyết trò chơi để lí giải và suy đoán một số ít tác dụng của học thuyết tiến hoá .Lí thuyết trò chơi đã trở thành một trong những công cụ nghiên cứu và phân tích tiêu chuẩn của kinh tế tài chính học. Trước mắt đều có ứng dụng rộng khắp ở kinh tế tài chính học, sàn chứng khoán học, sinh vật học, kinh tế tài chính học, quan hệ quốc tế, khoa học máy tính, chính trị học, kế hoạch quân sự chiến lược và rất nhiều ngành học khác. [ 1 ] Nguồn gốc của lí thuyết trò chơi văn minh là do John von Neumann đưa ra sáng tạo độc đáo và chứng tỏ điểm cân đối của sách lược hỗn hợp so với trò chơi có tổng bằng không của hai người .

Biểu diễn trò chơi[sửa|sửa mã nguồn]

Các trò chơi được nghiên cứu trong ngành Lý thuyết trò chơi là các đối tượng toán học được định nghĩa rõ ràng. Một trò chơi bao gồm một tập các người chơi/đấu thủ, một tập các nước đi (hoặc chiến lược) mà người chơi có thể chọn, và một đặc tả về cơ chế thưởng phạt cho mỗi tổ hợp của các chiến lược. Có hai cách biểu diễn trò chơi thường thấy trong các tài liệu.

Xem thêm Danh sách những trò chơi trong Lý thuyết trò chơi .

Dạng chuẩn tắc[sửa|sửa mã nguồn]

Một trò chơi dạng chuẩn tắc
Đấu thủ 2 chọn cột trái
Đấu thủ 2 chọn cột phải
Đấu thủ 1 chọn hàng trên
4, 3
– 1, – 1
Đấu thủ 1 chọn hàng dưới
0, 0
3, 4

Trò chơi chuẩn tắc (hoặc dạng chiến lược (strategic form)) là một ma trận cho biết thông tin về các đấu thủ, chiến lược, và cơ chế thưởng phạt (xem ví dụ bên phải). Trong ví dụ, có hai đấu thủ, một người chọn hàng, người kia chọn cột. Mỗi đấu thủ có hai chiến lược, mỗi chiến lược được biểu diễn bởi một ô được xác định bởi số hiệu hàng và số hiệu cột của nó. Mức thưởng phạt được ghi trong ô đó. Giá trị thứ nhất là mức thưởng phạt cho đấu thủ chơi theo hàng (trong ví dụ là Đấu thủ 1); giá trị thứ hai là mức thưởng phạt cho đấu thủ chơi theo cột (trong ví dụ là Đấu thủ 2). Giả sử Đấu thủ 1 chơi hàng trên và Đấu thủ 2 chơi cột trái. Khi đó, Đấu thủ 1 nhận 4 điểm và Đấu thủ 2 nhận 3 điểm.

Khi một trò chơi được trình diễn bằng dạng chuẩn tắc, người ta coi rằng mỗi đấu thủ hành vi một cách đồng thời, hoặc tối thiểu không biết về hành vi của người kia. Nếu những đấu thủ có thông tin về lựa chọn của những đấu thủ khác, trò chơi thường được trình diễn bằng dạng lan rộng ra .

Dạng lan rộng ra[sửa|sửa mã nguồn]

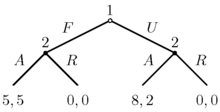Một trò chơi dạng lan rộng raCác trò chơi dạng lan rộng ra cố gắng nỗ lực miêu tả những trò chơi có thứ tự quan trọng. Ở đây, những trò chơi được trình diễn bằng cây ( như trong hình bên trái ). Mỗi đỉnh ( hoặc nút ) trình diễn một điểm mà người chơi hoàn toàn có thể lựa chọn. Người chơi được chỉ rõ bằng một số ít ghi cạnh đỉnh. Các đoạn thẳng đi ra từ đỉnh đó màn biểu diễn những hành vi hoàn toàn có thể cho người chơi đó. Mức thưởng phạt được ghi rõ tại đáy cây .

Trong trò chơi trong hình, có hai người chơi. Đấu thủ 1 đi trước và chọn F hoặc U. Đấu thủ 2 nhìn thấy nước đi của Đấu thủ 1 và chọn A hoặc R. Giả sử Đấu thủ 1 chọn U và sau đó Đấu thủ 2 chọn A. Khi đó, Đấu thủ 1 được 8 điểm và Đấu thủ 2 được 2 điểm.

Các trò chơi lan rộng ra còn hoàn toàn có thể diễn đạt những trò chơi đi-đồng-thời. Hoặc có một đường chấm chấm hoặc một đường tròn vẽ quanh hai đỉnh khác nhau để trình diễn rằng chúng đều thuộc cùng một tập hợp thông tin ( nghĩa là, người chơi không biết họ đang ở điểm nào ) .

Các loại trò chơi[sửa|sửa mã nguồn]

Trò chơi đối xứng và bất đối xứng[sửa|sửa mã nguồn]

Một trò chơi bất đối xứng
E
F
E

1, 2

0, 0

F

0, 0

1, 2

Một trò chơi đối xứng là một trò chơi mà phần lợi cho việc chơi một giải pháp nào đó chỉ nhờ vào vào những giải pháp được sử dụng, chứ không nhờ vào vào người nào đang chơi. Nếu như tính danh của những người chơi hoàn toàn có thể đổi khác mà không làm biến hóa phần lợi so với giải pháp chơi, thì một trò chơi là đối xứng. Nhiều trò chơi 2 × 2 thường được điều tra và nghiên cứu là đối xứng. Những màn biểu diễn chuẩn của trò chơi con gà, song đề tù nhân, đi săn nai là những trò chơi đối xứng .Đa số những trò chơi bất đối xứng được điều tra và nghiên cứu là những trò chơi mà những tập hợp giải pháp khác nhau được sử dụng bởi hai người chơi. Chẳng hạn, trò chơi tối hậu thư và tựa như như vậy trò nhà độc tài có giải pháp khác nhau cho mỗi người chơi. Tuy vậy, hoàn toàn có thể xảy ra trường hợp một trò chơi có những giải pháp giống nhau cho cả hai người chơi, nhưng vẫn bất đối xứng. Chẳng hạn, trò chơi được minh họa bên phải là bất đối xứng mặc dầu cho có cùng tập những giải pháp cho cả hai người chơi .

Trò chơi tổng bằng không và trò chơi tổng khác không[sửa|sửa mã nguồn]

Một trò chơi tổng bằng 0
A
B
A

2, −2

−1, 1

B

−1, 1

3, −3

Trong trò chơi tổng bằng không, với mọi tổng hợp của những kế hoạch chơi, tổng điểm của tổng thể những người chơi trong ván chơi luôn bằng 0. Nói một cách không chính thức, đấu thủ này hưởng lợi trên thiệt hại của những đấu thủ khác. Một ví dụ là trò Poker, trong đó người này thắng số điểm bằng đúng số điểm mà người kia thua. Các loại cờ cổ xưa như cờ vây, cờ vua và cờ tướng cũng là những trò chơi tổng bằng không Nhiều trò chơi mà những nhà lý thuyết trò chơi điều tra và nghiên cứu, trong đó có song đề tù nhân nổi tiếng, là những trò chơi tổng khác không, do có một số ít kết cục có tổng kết quả lớn hơn hoặc nhỏ hơn không. Nói một cách không chính thức, trong những trò chơi tổng khác không, một thu hoạch của đấu thủ này không nhất thiết tương ứng với một thiệt hại của một đấu thủ khác. Có thể biến hóa một trò chơi bất kể thành một trò chơi tổng bằng không bằng cách bổ trợ một đấu thủ ” bù nhìn ” sao cho những thiệt hại của đấu thủ này bù lại tổng thu hoạch của những đấu thủ khác .

Trò chơi đồng thời và trò chơi tuần tự[sửa|sửa mã nguồn]

Trong các trò chơi đồng thời (simultaneous game), cả hai đấu thủ thực hiện các nước đi một cách đồng thời, hoặc nếu không thì đấu thủ này sẽ không biết về các hành động trước đó của các đối thủ khác (và như vậy cũng tạo “hiệu ứng” đồng thời). Trong các trò chơi tuần tự (sequential game), người đi sau có biết một số (nhưng không nhất thiết toàn bộ) thông tin về các nước đi trước.

Biểu diễn dạng chuẩn tắc được dùng để trình diễn những trò chơi đồng thời, còn Biểu diễn dạng lan rộng ra được dùng cho những trò chơi tuần tự .

Trò chơi thông tin tuyệt vời và Trò chơi có thông tin không tuyệt vời và hoàn hảo nhất[sửa|sửa mã nguồn]

A game of imperfect information ( the dotted line represents ignorance on the part of player 2 )

Các trò chơi thông tin hoàn hảo (games of perfect information) lập thành một tập con quan trọng của các trò chơi tuần tự. Một trò chơi được gọi là có thông tin hoàn hảo nếu mọi đấu thủ biết tất cả các nước đi mà tất cả các đấu thủ khác đã thực hiện. Do vậy chỉ có các trò chơi tuần tự mới có thể là các trò chơi thông tin hoàn hảo. Hầu hết các trò chơi được nghiên cứu trong lý thuyết trò chơi là các trò chơi thông tin không hoàn hảo, tuy một số trò chơi hay như cờ vây, cờ vua lại là trò chơi thông tin hoàn hảo.

Tính chất thông tin tuyệt đối thường bị nhầm lẫn với khái niệm thông tin rất đầy đủ. Tính chất thông tin rất đầy đủ yên cầu rằng mỗi người chơi biết về những kế hoạch và thành quả thu được của những người chơi khác, nhưng không nhất thiết biết về những hành vi của họ .

Các trò chơi dài vô tận[sửa|sửa mã nguồn]

Bởi các lý do hiển nhiên, các trò chơi được nghiên cứu bởi các kinh tế gia và những người chơi trong thế giới thực nhìn chung là kết thúc trò chơi trong hữu hạn các bước đi. Các nhà toán học lý thuyết không bị cản trở bởi điều đó, và lý thuyết gia về tập hợp đặc biệt nghiên cứu về các trò chơi kết thúc sau vô hạn các bước đi, bới người thắng (hay là phần lợi) là không biết được cho đến sau khi các bước đi đó đã hoàn thành.

Sự chú ý thường không phải là quá nhiều về cách nào tốt nhất để chơi trò chơi, mà đơn giản là chỉ phụ thuộc vào người chơi hay người kia có hay không một chiến thuật chiến thắng. (Có thể chứng minh rằng, sử dụng tiên đề chọn lựa,là có những trò chơi với—ngay cả là đầy đủ thông tin hoàn toàn, và chỉ có kết quả là “thắng” hay “thua”— và không người chơi nào có chiến thuật để chiến thắng.) Sự tồn tại của những chiến thuật như vậy, cho những trò chơi được thiết kế một cách thông minh, có những kết quả quan trọng trong lý thuyết miêu tả tập hợp.

Ứng dụng của lý thuyết trò chơi[sửa|sửa mã nguồn]

Các trò chơi trong dạng này hay dạng khác được sử dụng thoáng rộng trong nhiều ngành điều tra và nghiên cứu khác nhau .

Kinh tế và kinh doanh thương mại[sửa|sửa mã nguồn]

Các nhà kinh tế tài chính học đã sử dụng lý thuyết trò chơi để nghiên cứu và phân tích một diện rộng những hiện tượng kỳ lạ kinh tế tài chính, trong đó có đấu giá, mặc cả, duopoly và oligopoly, những tổ chức triển khai mạng lưới xã hội và những mạng lưới hệ thống bầu cử. Nghiên cứu này thường tập trung chuyên sâu vào một tập đơn cử những kế hoạch được biết với tên những trạng thái cân đối trong trò chơi. Nổi tiếng nhất là cân đối Nash của nhà toán học John Nash, người đã được phần thưởng Nobel cho khu công trình nghiên cứu và điều tra của ông về lý thuyết trò chơi .
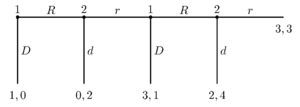A three stage Centipede GameCông dụng tiên phong là để phân phối thông tin cho tất cả chúng ta về việc là hàng loạt dân số sẽ thực sự hành xử như thế nào. Một số học giả tin rằng bằng cách tìm ra những điểm cân đối của những trò chơi họ hoàn toàn có thể Dự kiến được dân số sẽ hành xử như thế nào khi đối phó với những trường hợp giống như trò chơi đang được nghiên cứu và điều tra. Quan điểm đặc biệt quan trọng này về lý thuyết trò chơi đã bị chỉ trích gần đây. Thứ nhất, nó bị chỉ trích chính bới những giả sử được ra bởi những lý thuyết gia trò chơi thường bị vi phạm. Một số lý thuyết gia trò chơi hoàn toàn có thể giả sử rằng những người chơi luôn hành xử hài hòa và hợp lý để làm tối ưu hóa phần thắng của anh ta ( quy mô Homo economicus ), nhưng người thật thường hành vi hoặc là không hài hòa và hợp lý, hoặc là hành vi hài hòa và hợp lý để là tối ưu phần thắng của một nhóm người lớn hơn ( hành vi vị tha ). Những lý thuyết gia trò chơi vấn đáp bằng cách so sánh những giả sử của họ với những giả sử được sử dụng trong vật lý. Do vậy trong khi những giả sử của họ không phải luôn luôn đúng, họ hoàn toàn có thể xem lý thuyết trò chơi như thể một lý tưởng khoa học hài hòa và hợp lý giống như là những quy mô được sử dụng bởi những nhà vật lý. Tuy nhiên, những chỉ trích thêm của việc sử dụng này của lý thuyết trò chơi đã được giảm đi chính do một số ít thí nghiêm cho thấy rằng những cá thể không chơi những kế hoạch cân đối. Ví dụ, trong trò chơi Centipede, Đoán 2/3 trung bình, và trò Nhà độc tài, người ta thường không chơi với cân đối Nash. Sự tranh cãi vẫn tiếp nối tương quan đến sự quan trọng của những thí nghiệm này .Thay vào đó, 1 số ít tác giả cho rằng cân đối Nash không đưa ra những Dự kiến cho toàn dân số con người, nhưng thiên về cung ứng một lời lý giải tại sao những dân số chơi theo cân đối Nash vẫn duy trì ở trong trạng thái đó. Tuy nhiên, câu hỏi tại sao dân số đạt đến những điểm đó vẫn là bài toán mở .Một số lý thuyết gia trò chơi đã xoay qua lý thuyết tiến hóa trò chơi để lý giải những lo ngại này. Những quy mô này giả sử hoặc là không có sự hài hòa và hợp lý nào hoặc là hài hòa và hợp lý bị chặn trên phần của những người chơi. Mặc cho tên gọi, lý thuyết tiến hóa trò chơi không thiết yếu giả sử tinh lọc tự nhiên theo nghĩa của sinh học. Lý thuyết tiến hóa trò chơi gồm có cả sinh học cũng như là tiến hóa văn hóa truyền thống và cũng như những quy mô học tập cá thể ( ví dụ, dịch chuyển của trò chơi giả ) .

Tính quy chuẩn[sửa|sửa mã nguồn]

Song đề tù nhân
Hợp tác
Phản bội
Hợp tác

2, 2

0, 3

Phản bội

3, 0

1, 1

Theo quan điểm khác, 1 số ít học giả cho rằng lý thuyết trò chơi không phải là một công cụ Dự kiến cho hành vi của con người, mà như thể một ý kiến đề nghị để người ta nên phải hành xử như thế nào. Bởi vì một cân đối Nash của một trò chơi gồm có những đáp lại tốt nhất cho những hành vi của những người chơi khác, chơi một giải pháp là một phần của một cân đối Nash trông có vẻ như là hài hòa và hợp lý. Tuy nhiên, việc sử dụng này của lý thuyết trò chơi cũng đã bị chỉ trích. Đầu tiên, trong 1 số ít trường hợp là hài hòa và hợp lý để chơi một kế hoạch không cân đối nếu như một người mong đợi những người khác cũng chơi những kế hoạch không cân đối. Ví dụ, xem Đoán 2/3 giá trị trung bình .Thứ hai là, Song đề tù nhân đưa ra một phản ví dụ điển hình nổi bật khác. Trong Song đề tù nhân, mỗi người chơi đi theo sở trường thích nghi riêng của anh ta dẫn đến cả hai người chơi đều bị thiệt thòi thêm nếu như họ không theo đuổi những sở trường thích nghi riêng của họ. Một số học giả tin rằng điều này trình diễn sự thất bại của lý thuyết trò chơi như thể một khuyến nghị cho hành xử .
Diều hâu – Bồ câu
Diều hâu
Bồ câu
Diều hâu

(V-C)/2, (V-C)/2

V, 0

Bồ câu

0, V

V/2, V/2

Không giống như trong kinh tế, phần lợi cho những trò chơi trong sinh học thường được diễn dịch như là tương ứng với sự thích nghi. Thêm vào đó, chú ý đã ít hơn về các cân bằng có liên quan đến khái niệm của sự hợp lý, nhưng là thiên về những thứ có thể duy trì được bởi các lực tiến hóa. Cân bằng được biết đến nhiều nhất trong sinh học được biết đến như là chiến lược tiến hóa bền vững (viết tắt ESS cho Evolutionary Stable Strategy), là được giới thiệu lần đầu bởi John Maynard Smith (mô tả trong cuốn sách năm 1982 của ông). Mặc đu động lực ban đầu của nó không liên quan đến bất cứ yêu cầu về tinh thần nào của cân bằng Nash, mỗi ESS là một cân bằng Nash.

Trong sinh học, lý thuyết trò chơi đã được sử dụng để hiểu được nhiều hiện tượng kỳ lạ khác nhau. Nó được sử dụng lần đầu để lý giải sự tiến hóa ( và bền vững và kiên cố ) của tỷ suất giới tính khoảng chừng 1 : 1. Ronald Fisher ( 1930 ) đề xuất rằng tỉ lệ giới tính 1 : 1 là tác dụng của những lực tiến hóa tác động ảnh hưởng lên những cá thể là những người hoàn toàn có thể được xem như thể cố gắng nỗ lực làm tối đa số cháu chắt của mình .Thêm vào đó, những nhà sinh vật đã sử dụng lý thuyết trò chơi tiến hóa và ESS để lý giải sự nổi lên của liên lạc giữa muông thú ( Maynard Smith và Harper, 2003 ). Sự nghiên cứu và phân tích của những trò chơi tín hiệu và những trò chơi liên lạc khác đã cung ứng một số ít trực giác vào trong sự tiến hóa của việc liên lạc giữa muôn thú .Cuối cùng, những nhà sinh vật đã sử dụng trò chơi diều hâu-bồ câu ( cũng được biết đến như là con gà ) để nghiên cứu và phân tích những hành vi đánh nhau và tranh giành chủ quyền lãnh thổ .

Khoa học máy tính và logic[sửa|sửa mã nguồn]

Lý thuyết trò chơi đã đóng một vai trò ngày càng quan trọng trong logic và trong khoa học máy tính. Một số lý thuyết logic có cơ sở trong ngữ nghĩa trò chơi. Thêm vào đó, những khoa học gia máy tính đã sử dụng trò chơi để mô phỏng những đo lường và thống kê tương tác với nhau .

Chính trị học[sửa|sửa mã nguồn]

Các điều tra và nghiên cứu trong khoa học chính trị cũng có sử dụng lý thuyết trò chơi. Một thuyết trò chơi lý giải cho lý thuyết dân chủ độc lập rằng tính công khai minh bạch và tranh luận cởi mở trong những nền dân chủ sẽ gởi một thông điệp rõ ràng và khả tín về những tiềm năng đến những chính sách khác. trái lại, khó mà biết được những chủ đích của những chỉ huy phi dân chủ ( độc tài ), rằng sẽ có sự nhượng bộ chung hiệu suất cao nào, và những lời hứa hẹn có được tôn trọng hay không. Do đó, sẽ sống sót vấn đề không tin yêu và không mong ước nhằm mục đích tạo ra sự nhượng bộ chung nếu tối thiểu một trong những thành phần của sự bàn cãi này là thành phần phi dân chủ .. [ 3 ]
Lý thuyết trò chơi đã được đưa vào một vài sử dụng trong triết học. Hai bài báo bởi W.V.O. Quine ( 1960, 1967 ), David Lewis ( 1969 ) sử dụng lý thuyết trò chơi để tăng trưởng một triết lý của hội nghị. Khi thao tác đó, ông đã cung ứng những nghiên cứu và phân tích tiên phong của kiến thức và kỹ năng chung và sử dụng nó trong việc nghiên cứu và phân tích những cách chơi trong những trò chơi được quản trị. Thêm vào đó, ông lần tiên phong đề xuất rằng người ta hoàn toàn có thể hiểu được ý nghĩa dưới những điều kiện kèm theo của trò chơi đánh tín hiệu. Đề nghị sau đã được theo đuổi bởi một vài triết gia tính từ Lewis ( Skyrms 1996, Grim et al. 2004 ) .
Trò săn nai
Nai
Thỏ
Nai

3, 3

0, 2

Thỏ

2, 0

2, 2

Trong đạo đức, một số ít tác giả đã cố gắng nỗ lực theo đuổi dự án Bất Động Sản này, mở màn bởi Thomas Hobbes, bằng cách suy diễn ra đạo đức từ những quyền lợi cá thể. Bởi vì những trò chơi giống như Prisoner’s Dilemma đưa ra những xích míc rõ ràng giữa đạo đức và quyền lợi cá thể, lý giải tại sao hợp tác là thiết yếu bởi quyền lợi cá thể là một phần quan trọng của dự án Bất Động Sản này. Chiến lược chung này là một phần của quan điểm hợp đồng xã hội tổng quát trong triết học chính trị ( ví dụ điển hình, xem Gauthier 1987 và Kavka 1986 ) .Cuối cùng, một số ít tác giả khác đã cố gắng nỗ lực sử dụng lý thuyết tiến hóa trò chơi để lý giải sự tăng trưởng trong quan điểm con người về đạo đức và những hành xử tương ứng của muông thú. Những tác giả này đã xem xét 1 số ít trò chơi gồm có Song đề tù nhân, săn nai, và trò mặc cả của Nash như để phân phối một lời lý giải về sự tăng trưởng của những quan điểm về đạo đức ( xem, e. g., Skyrms 1996, 2004 ; Sober và Wilson 1999 ) .

Lịch sử của ngành Lý thuyết trò chơi[sửa|sửa mã nguồn]

Những thảo luận đầu tiên được biết đến về lý thuyết trò chơi xuất hiện trong một lá thư viết bởi James Waldegrave vào năm 1713. Trong lá thư này, Waldegrave đưa ra lời giải chiến thuật hỗn hợp minimax cho một trò đánh bài hai người chơi le Her. Chỉ đến khi sự xuất bản Nghiên cứu về những Định luật toán học của lý thuyết Tài sản của Antoine Augustin Cournot vào năm 1838 thì những phân tích chung về lý thuyết trò chơi mới được theo đuổi. Trong tác phẩm này Cournot xem xét duopoly và đưa một phiên bản giới hạn của cân bằng Nash.

Mặc dù những phân tích của Cournot là tổng quát hơn là của Waldegrave, lý thuyết trò chơi chưa thật sự tồn tại như là một ngành duy nhất cho đến khi John von Neumann xuất bản một loạt các bài báo vào năm 1928. Những kết quả này sau này được mở rộng thêm ra trong cuốn sách xuất bản năm 1944 Lý thuyết trò chơi và các hành vi kinh tế bởi von Neumann và Oskar Morgenstern. Tác phẩm uyên thâm này chứa đựng phương pháp tìm những lời giải tối ưu cho những trò chơi tổng bằng không với hai người chơi. Trong suốt khoảng thời gian này, những tác phẩm về lý thuyết trò chơi chủ yếu tập trung vào lý thuyết các trò chơi hợp tác, phân tích về những chiến thuật tối ưu cho một nhóm các cá nhân, giả sử rằng họ có thể bảo đảm những thỏa thuận giữ họ với những chiến thuật thích hợp.

Vào năm 1950, đàm đạo tiên phong của Prisoner’s dilemma Open, và một thí nghiệm được làm về trò chơi này tại công ty RAND. Vào khoảng chừng cùng thời hạn đó, John Nash tăng trưởng một định nghĩa về một giải pháp ” tối ưu ” cho những trò chơi với nhiều người chơi, và chưa một tối ưu nào được định nghĩa trước đó, được biết đến như là cân đối Nash. Cân bằng này là đủ tổng quát, được cho phép sự nghiên cứu và phân tích về trò chơi không hợp tác thêm vào những trò chơi có hợp tác .Lý thuyết trò chơi trải qua một thời hạn sôi động trong những năm 1950, trong những năm đó những khái niệm về cốt lõi, dạng trò chơi bao quát, trò chơi giả, trò chơi lặp, và giá trị Shapley được tăng trưởng. Thêm vào đó, những ứng dụng tiên phong của lý thuyết trò chơi vào triết học và khoa học chính trị diễn ra trong thời hạn này .Vào năm 1965, Reinhard Selten ra mắt khái niệm lời giải của những cân đối lý tưởng của những trò chơi con, làm đúng mực thêm cân đối Nash equilibrium ( sau đó cũng ông trình làng sự triển khai xong rung tay ). Vào năm 1967, John Harsanyi tăng trưởng những khái niệm thông tin trọn vẹn và trò chơi Bayesian. Ông ta, cùng với John Nash và Reinhard Selten, đoạt phần thưởng Nobel về kinh tế tài chính vào năm 1994 .

Trong những năm 1970, lý thuyết trò chơi được áp dụng rộng rãi vào sinh học, chủ yếu là do kết quả của các công trình của John Maynard Smith và chiến lược tiến hóa bền vững của ông. Thêm vào đó, những khái niệm về cân bằng liên quan, sự hoàn toàn rung tay, và kiến thức chung được giới thiệu và phân tích.

Vào năm 2005, những lý thuyết gia trò chơi Thomas Schelling và Robert Aumann đoạt giải thưởng Nobel về kinh tế. Schelling là về các mô hình động, các ví dụ ban đầu của lý thuyết tiến hóa trò chơi. Aumann đóng góp thêm vào trường cân bằng (equilibrium school), phát triển một cân bằng làm thô đi những cân bằng liên quan nhau và phát triển các phân tích chi tiết về giả sử của kiến thức chung.

1. ^ a b Vương, Đức Lượng. Nghiên cứu lí luận hướng tâm trong bài thuyết trình. Beijing Book Co. Inc., 2015. ISBN 7513561621.

Giáo trình và các sách tham khảo tổng quan

• Bierman, H. S. and L. Fernandez, Game Theory with economic applications, Addison-Wesley, 1998.
• Fudenberg, Drew and Jean Tirole: Game Theory, MIT Press, 1991, ISBN 0-262-06141-4 (the definitive reference text)
• Gibbons, Robert (1992) Game Theory for Applied Economists, Princeton University Press ISBN 0-691-00395-5 (readable; suitable for advanced undergraduates. Published in Europe by Harvester Wheatsheaf (London) with the title A primer in game theory)
• Ginits, Herbert (2000) Game Theory Evolving Princeton University Press ISBN 0-691-00943-0
• Osborne, Martin and Ariel Rubinstein: A Course in Game Theory, MIT Press, 1994, ISBN 0-262-65040-1 (modern introduction at the introductory graduate level)
• Rasmusen, Erik: Games and information, 4th edition, Blackwell, 2006. Available online [6].

Sách có tính lịch sử

Các sách tham khảo khác

Các website

Source: https://mindovermetal.org
Category: Ứng dụng hay