Ứng dụng thực tế các tỉ số lượng giác của góc nhọn. Thực hành ngoài trời

1. Xác định chiều cao

a) Nhiệm vụ

Xác định độ cao của một tháp mà không cần lên đỉnh của tháp .
b ) Chuẩn bị :
Giác kế, thước cuộn, máy tính bỏ túi ( hoặc bảng lượng giác ) .
c ) Hướng dẫn thực thi ( h. 34 )

Đặt kế giác thẳng đứng cách chân tháp một khoảng chừng USD a USD USD ( CD = a ) USD, giả sử chiều cao của giác kế là USD b USD USD ( OC = b ). USD
Quay thanh giác kế sao cho khi ngắm theo thanh ta nhìn thấy đỉnh USD A $ của tháp. Đọc trên giác kế số đo \ ( \ alpha \ ) của góc USD AOB USD .
Dùng bảng lượng giác hoặc máy tính bỏ túi để tính \ ( tg \ alpha \ ). Tính tổng \ ( b + a \ cdot tg \ alpha \ ) và báo tác dụng .

2. Xác định khoảng cách

a ) Nhiệm vụ
Xác định chiều rộng của một khúc sông mà việc đo đạc chỉ triển khai tại một bờ sông .
b ) Chuẩn bị
Ê-ke đạc, giác kế, thước cuộn, máy tính bỏ túi hoặc bảng lượng giác .
c ) HƯớng dẫn triển khai ( h. 35 )

Ta có hai bờ sông song song với nhau .
Chọn một điểm USD B USD phía bên kia sông. Lấy một điểm USD A $ bên này sông sao cho vuông góc với các bờ sông .
Dùng ê-ke đạc kẻ đường thẳng USD Ax USD phía bên này sông sao cho \ ( Ax \ perp AB \ ) .
Lấy điểm USD C USD trên USD Ax USD, giả sử USD AC = a USD. Dùng giác kế đo góc USD Ngân Hàng Á Châu USD, giả sử : \ ( \ widehat { Ngân Hàng Á Châu } = \ alpha \ ) .Dùng máy tính bỏ túi hoặc bảng lượng giác để tính \ ( tg \ alpha \ ) .
Tính tích \ ( a \ cdot tg \ alpha \ ) và báo tác dụng .
Khi đó chiều rộng khúc sông AB chính là giá trị của : \ ( a.tan \ alpha \ )

3. Ví dụ

Ví dụ 1:

Tính độ cao của một cây xanh biết rằng một người cao USD 1,7 m USD đứng nhìn lên đỉnh cây thì hướng nhìn tạo với mặt đất góc USD 35 $ độ và khoảng cách từ người đó đến cây là USD 20 m USD .

Bài giải:

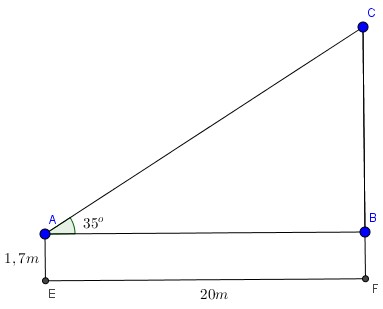
Ta xem đề bài giống như hình vẽ trên \ ( \ widehat { ABC } = 90 ^ { \ circ } \ )
Khi đó chiều cao cây cần tính là đoạn :
USD CF = CB + BF = AB.tan 35 ^ { \ circ } + AE USD
USD = 20. tan35 ^ { \ circ } + 1,7 \ simeq 15,7 ( m ) USD

Ví dụ 2:

Một cái cây bị sét đánh trúng giữa thân cây làm thân cây ngã xuống đất tạo với mặt đất một góc là \ ( 40 ^ { \ circ } \ ). Biết rằng khúc thân cây còn đứng cao USD 3 m USD .

Tính chiều cao lúc đầu của câ.

Bài giải:

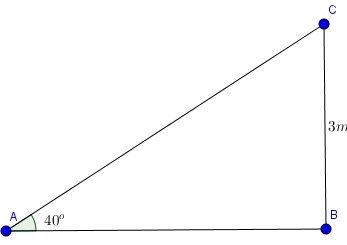
Ta xem đề bài như hình vẽ với \ ( \ widehat { ABC } = 90 ^ { \ circ } \ )
Khi đó chiều dài cây lúc đầu chính là :
USD BC + AC = BC + \ frac { BC } { sinA } USD
USD = 3. ( 1 + \ frac { 1 } { sin40 ^ { \ circ } } ) \ simeq 7,67 ( m ) USD

Ví dụ 3:

Một chiếc thang gấp đôi dài USD 6 m USD được người ta sử dụng để leo lên một mái nhà. Biết rằng lúc leo lên mỗi chân thang tạo với mặt đất góc USD 60 ^ 0 USD độ .
Tính chiều cao của căn nhà đó .

Bài giải:

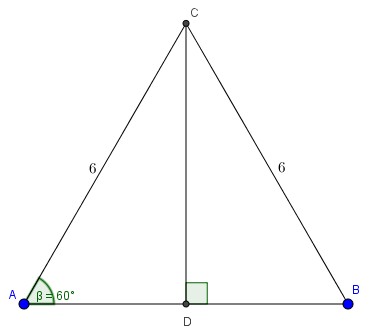
Ta xem đề bài như hình vẽ trên :
Khi đó ta có \ ( \ Delta ABC \ ) đều và \ ( CD = AC.sin 60 ^ { \ circ } = 6. \ frac { \ sqrt { 3 } } { 2 } = 3 \ sqrt { 3 } \ )

Ví dụ 4:

Ở một cái thang đơn dài USD 3 m USD có ghi “ để bảo vệ bảo đảm an toàn cần đặt thang sao cho góc tạo thành so với mặt đất là \ ( \ alpha \ ) thì phải thỏa mãn nhu cầu \ ( 60 ^ { \ circ } < \ alpha < 75 ^ { \ circ } \ ). Vậy phải đặt thang cách vật thang dựa khoảng chừng bao nhiêu để bảo vệ bảo đảm an toàn .

Bài giải:

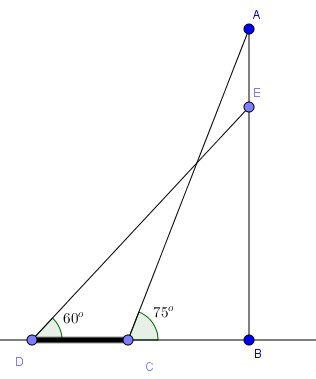
Ta xem đề bài như hình vẽ trên :
Khi đó : Khoảng bảo đảm an toàn là nằm trong khoảng chừng từ USD C USD đến USD D USD .
Ta có :
\ ( BC = AC.cos 75 ^ { \ circ } = 3. cos75 ^ { \ circ } \ simeq 0,776 ( m ) \ ) ;
\ ( BD = ED.cos 60 ^ { \ circ } = 3. cos60 ^ { \ circ } = 1,5 ( m ) \ )

Vậy phải đặt thang cách vật dựa một đoạn là \(l(m)\) thỏa mãn: \(0,776(m)

Ví dụ 5:

Cho tam giác USD ABC USD vuông tại USD B USD có \ ( BC = 20 m, \ widehat { BCA } = 50 ^ { \ circ } \ ). Một đường thẳng song song với USD BC USD cắt USD AB, AC $ lần lượt tại USD D, E. USD
Biết rằng USD BD = 5 m USD. Độ dài USD AE USD là : ?

Bài giải:

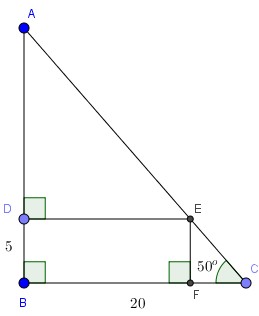
Khi đó :
\ ( AC = \ frac { BC } { cos50 ^ { \ circ } } = \ frac { 20 } { cos50 ^ { \ circ } } \ simeq 31,11 ( m ) \ ), \ ( BD = EF \ )
USD EC = \ frac { EF } { sin50 ^ { \ circ } } = \ frac { 5 } { sin50 ^ { \ circ } } \ simeq 6,53 ( m ) USD
USD \ Rightarrow AE = AC-EC = 24,58 ( m ) USD

Bài trước:

Bài tiếp theo:

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với bài Ứng dụng thực tế các tỉ số lượng giác của góc nhọn sgk toán 9 tập 1 !
“ Bài tập nào khó đã có giaibaisgk.com “

Source: https://mindovermetal.org
Category: Ứng dụng hay